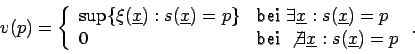Seminararbeit aus Angewandter Statistik
Klassische schließende Statistik für unscharfe Daten
Inhalt
- Inhalt
- Punktschätzung für Parameter
- Konfidenzbereiche für Parameter
- Nichtparametrische Schätzung
- Statistische Tests bei unscharfen Daten
- Literatur
Punktschätzung für Parameter
Dieser Abschnitt befaßt sich mit einer Verallgemeinerung der Punktschätzung
für den Parameter ![]() eines stochastischen Modells
eines stochastischen Modells
![]() mit dem Parameter
mit dem Parameter ![]() und Beobachtungsraum
und Beobachtungsraum ![]() für
für ![]() für unscharfe Daten.
für unscharfe Daten.
Die Schätzfunktion
![]() für den
Parameter
für den
Parameter ![]() ist eine meßbare Funktion, die den Stichprobenraum
ist eine meßbare Funktion, die den Stichprobenraum
![]() in
in ![]() abbildet, d.h.
abbildet, d.h.
Für Funktionen
![]() des Parameters
des Parameters ![]() mit
mit
kann eine Verallgemeinerung der Schätzfunktion für unscharfe Daten gegeben werden.
In diesem Fall sind die Schätzfunktionen
![]() von der
Form
von der
Form
- Beispiel 1.1:
- Für eine Normalverteilung
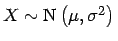 gilt
gilt
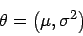
Eine wichtige, zu schätzende Funktion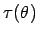 des Parameters
des Parameters
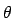 ist
ist
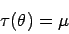
mit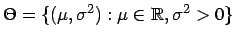 und
und
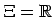
Punktschätzung bei unscharfen Daten
Ist
![]() eine Schätzfunktion eines gerafften Parameters
eine Schätzfunktion eines gerafften Parameters
![]() basierend auf einer Stichprobe
basierend auf einer Stichprobe
![]() einer stochastischen Größe
einer stochastischen Größe ![]() , so erhält man für die beobachteten Werte
, so erhält man für die beobachteten Werte
![]() einen Schätzwert
einen Schätzwert
Für unscharfe Beobachtungen
![]() muß eine brauchbare
Verallgemeinerung einer Schätzfunktion zu einem unscharfen Schätzwert
muß eine brauchbare
Verallgemeinerung einer Schätzfunktion zu einem unscharfen Schätzwert
![]() für
für
![]() führen.
führen.
Um einen unscharfen Schätzwert zu ermitteln, verwendet man die charakterisierenden
Funktionen
![]() der Beobachtungen
der Beobachtungen
![]() .
Diese werden mit einer passenden Regel kombiniert um so das unscharfe kombinierte
Stichprobenelement
.
Diese werden mit einer passenden Regel kombiniert um so das unscharfe kombinierte
Stichprobenelement
![]() des Stichprobenraumes
des Stichprobenraumes ![]() zu erhalten. Dieses unscharfe kombinierte Stichprobenelement ist ein unscharfer
Vektor mit der vektorcharakterisierenden Funktion
zu erhalten. Dieses unscharfe kombinierte Stichprobenelement ist ein unscharfer
Vektor mit der vektorcharakterisierenden Funktion
![]() gegeben durch
gegeben durch
Das unscharfe kombinierte Stichprobenelement ist die Basis für die Konstruktion einer unscharfen Verallgemeinerung von Schätzfunktionen für
- Definition 1.1:
- Ist
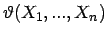 eine Schätzfunktion
für den Parameter
eine Schätzfunktion
für den Parameter 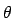 eines stochastischen Modells
eines stochastischen Modells
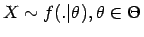 basierend auf einer Stichprobe
basierend auf einer Stichprobe
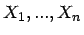 von
von 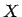 , so ist für
die unscharfen Beobachtungen
, so ist für
die unscharfen Beobachtungen
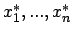 ein unscharfer Schätzwert
ein unscharfer Schätzwert
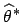 für
für 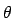 basierend auf dem unscharfen
kombinierten Stichprobenelement
basierend auf dem unscharfen
kombinierten Stichprobenelement
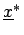 gegeben durch ein unscharfes
Element
gegeben durch ein unscharfes
Element
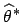 des Parameterraumes mit der charakterisierenden
Funktion
des Parameterraumes mit der charakterisierenden
Funktion 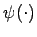 , für die gilt
, für die gilt
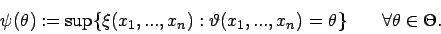
Um das Supremum![[*]](foot_motif.gif) zu ermitteln, müssen alle Elemente
zu ermitteln, müssen alle Elemente
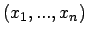 des Stichprobenraumes
berücksichtigt werden, die die Bedingung erfüllen. Verwendet man die Bezeichnung
des Stichprobenraumes
berücksichtigt werden, die die Bedingung erfüllen. Verwendet man die Bezeichnung
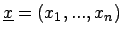 , kann man anschreiben:
, kann man anschreiben:
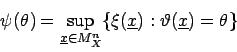
- Bemerkung:
- In der Stichprobe kann auch eine genaue Beobachtung
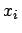 enthalten sein. In diesem Fall ist die entsprechende charakterisierende Funktion
enthalten sein. In diesem Fall ist die entsprechende charakterisierende Funktion
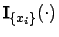 .
.
![[*]](cross_ref_motif.gif) erklärt das Prinzip
für eine Stichprobe mit
erklärt das Prinzip
für eine Stichprobe mit
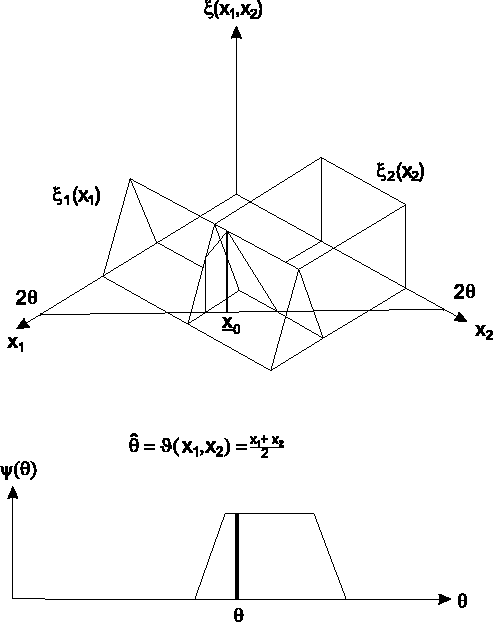
|
- Beispiel 1.2:
- Für das stochastische Modell
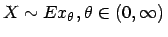 ,
d.h. für die Exponentialverteilung mit Dichtefunktion
,
d.h. für die Exponentialverteilung mit Dichtefunktion
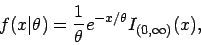
ist eine optimale Schätzfunktion (bezüglich Unverzerrtheit, Effizienz, Konsistenz und Plausibilität) für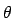 basierend auf einer exakten Stichprobe
basierend auf einer exakten Stichprobe
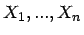 von
von 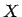 gegeben durch das Stichprobenmittel
gegeben durch das Stichprobenmittel
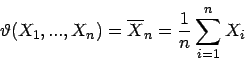
Für unscharfe Beobachtungen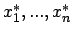 von
von 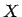 mit
dem unscharfen kombinierten Stichprobenelement
mit
dem unscharfen kombinierten Stichprobenelement
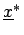 und
entsprechender vektorcharakterisierender Funktion
und
entsprechender vektorcharakterisierender Funktion
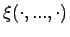 ist die charakterisierende Funktion
ist die charakterisierende Funktion 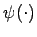 des unscharfen Schätzwertes
des unscharfen Schätzwertes
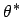 für
für 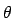 gegeben durch
gegeben durch
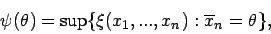
wobei das Supremum über dem Stichprobenraum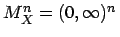 ermittelt werden muß.
ermittelt werden muß.
Abbildung![[*]](cross_ref_motif.gif) zeigt eine unscharfe Stichprobe
sowie die charakterisierenden Funktionen von zwei möglichen unscharfen Schätzwerten,
ermittelt mit verschiedenen Kombinationsregeln.
zeigt eine unscharfe Stichprobe
sowie die charakterisierenden Funktionen von zwei möglichen unscharfen Schätzwerten,
ermittelt mit verschiedenen Kombinationsregeln. -
Abbildung: Unscharfe Stichprobe einer Exponentialverteilung und die charakterisierenden Funktionen der Schätzwerte für den Mittelwert: Ausgehend von sechs gleichgestaltigen Beobachtungen wird ein Schätzwert für den Mittelwert berechnet. Im mittleren Bild ist das Ergebnis dargestellt, falls zur Kombination der einzelnen charakterisierenden Funktionen die Minimum-Kombinationsregel verwendet wird. Im unteren Bild wurde die Produkt-Kombinationsregel verwendet. Zu beachten ist, daß die Träger sowie die Bereiche für 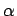 =1
übereinstimmen.
=1
übereinstimmen.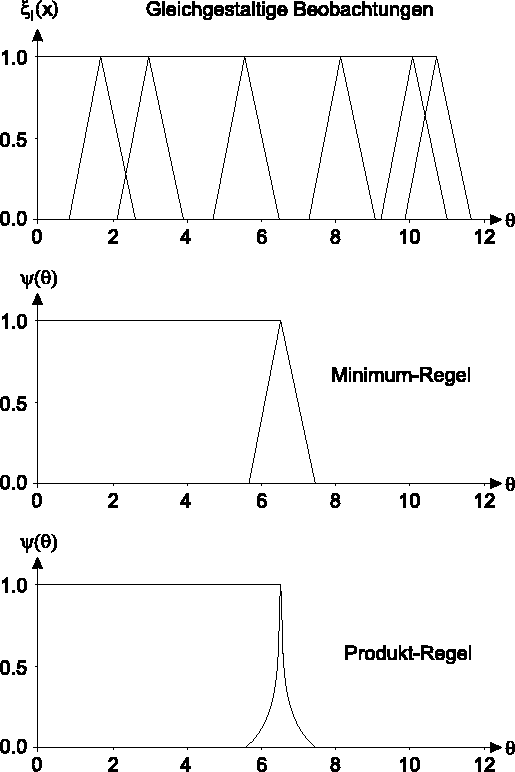
Punktschätzung für geraffte Parameter bei unscharfen Daten
Für Funktionen
![]() der Parameter eines stochastischen Modells
können durch Modifikation von Definition 1.1 unscharfe Schätzwerte gewonnen
werden.
der Parameter eines stochastischen Modells
können durch Modifikation von Definition 1.1 unscharfe Schätzwerte gewonnen
werden.
- Defintion 1.2:
- Unter den Annahmen von Definition 1.1 sei
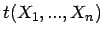 eine Schätzfunktion für
eine Schätzfunktion für
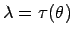 . Für unscharfe Beobachtungen
. Für unscharfe Beobachtungen
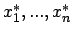 von
von 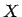 mit dem unscharfen kombinierten
Stichprobenelement
mit dem unscharfen kombinierten
Stichprobenelement
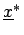 und der entsprechenden vektorcharakterisierenden
Funktion
und der entsprechenden vektorcharakterisierenden
Funktion
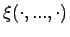 ist der unscharfe Schätzwert
ist der unscharfe Schätzwert
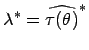 gegeben
durch seine charakterisierende Funktion
gegeben
durch seine charakterisierende Funktion 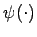
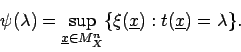
- Beispiel 1.3:
- Für
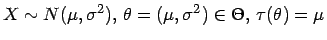 und einer unscharfen Stichprobe
und einer unscharfen Stichprobe
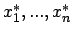 ist die charakterisierende
Funktion des unscharfen Schätzwertes
ist die charakterisierende
Funktion des unscharfen Schätzwertes
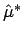 gegeben durch
gegeben durch
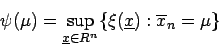
Ergänzende Beispiele
- Beispiel 1.4:
- Es ist zu zeigen, dass die gegebenen Definitionen bei exakten
Daten zur Indikatorfunktion des exakten Punktschätzers führen.
Dazu betrachtet man zuerst eine der Bedingungen, die eine gültige Kombinationsregel erfüllen muß:
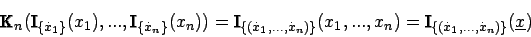
Wenn man nun die Indikatorfunktionen für exakte Daten verwendet, erhält man für die vektorcharakterisierende Funktion
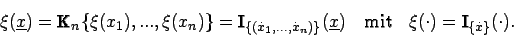
Für den Schätzwert ergibt sich daher
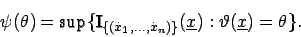
Mit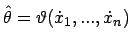 läßt sich dies
noch vereinfachen zu
läßt sich dies
noch vereinfachen zu
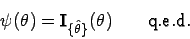
- Beispiel 1.5:
- Es ist zu zeigen, dass sich für Intervalldaten unabhängig von
der verwendeten Kombinationsregel derselbe unscharfe Schätzwert ergibt.
Die Kombinationsregeln sind wie folgt definiert:

Ausgehend von der charakterisierenden Funktion für Intervalldaten![\( \xi (\cdot )=\textrm{I}_{[a,b]}(\cdot ) \)](img76.gif) betrachtet man die Ergebnisse der Minimum- bzw. Produkt-Kombinationsregel für
zwei Beobachtungen in nachfolgender Tabelle.
betrachtet man die Ergebnisse der Minimum- bzw. Produkt-Kombinationsregel für
zwei Beobachtungen in nachfolgender Tabelle.
Man erkennt, dass die Ergebnisse für beide Kombinationsregeln übereinstimmen, d.h. es ergibt sich die gleiche vektorcharakterisierende Funktion. Da bei der Berechnung des unscharfen Schätzwertes mit der vektorcharakterisierenden Funktion weitergerechnet wird, die verwendete Kombinationsregel aber keinerlei Berücksichtigung findet, ist auch das Endergebnis unabhängig von der verwendeten Kombinationsregel. Diese Schlußfolgerung läßt sich für beliebig viele Beobachtungen anwenden.
|
|
|
Min. | Prod. |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
Konfidenzbereiche für Parameter
Bezeichnet ![]() die Potenzmenge und ist
die Potenzmenge und ist
![]() eine Konfidenzfunktion mit Überdeckungswahrscheinlichkeit
eine Konfidenzfunktion mit Überdeckungswahrscheinlichkeit ![]() für
den Parameter
für
den Parameter ![]() basierend auf einer Stichprobe
basierend auf einer Stichprobe
![]() der stochastischen Größe
der stochastischen Größe
![]() , d.h.
, d.h.
so muß gelten
Für eine konkrete beobachtete Stichprobe erhält man eine Teilmenge
![]() von
von ![]() .
.
Konfidenzbereiche bei unscharfen Daten
Im Fall von unscharfen Daten
![]() erhält man durch
eine Verallgemeinerung der Konfidenzbereiche eine unscharfe Teilmenge
des Parameterraumes auf folgende Art:
erhält man durch
eine Verallgemeinerung der Konfidenzbereiche eine unscharfe Teilmenge
des Parameterraumes auf folgende Art:
- Definition 2.1:
- Ist
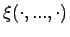 die vektorcharakterisierende
Funktion des unscharfen kombinierten Stichprobenelements und
die vektorcharakterisierende
Funktion des unscharfen kombinierten Stichprobenelements und
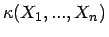 eine Konfidenzfunktion, so ist die charakterisierende Funktion
eine Konfidenzfunktion, so ist die charakterisierende Funktion
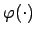 des verallgemeinerten Konfidenzbereiches gegeben durch
des verallgemeinerten Konfidenzbereiches gegeben durch
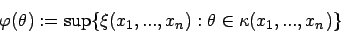
wobei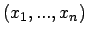 über den Stichprobenraum
über den Stichprobenraum 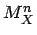 von
von
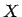 variiert wird.
variiert wird. - Bemerkung:
- Für diesen verallgemeinerten Konfidenzbereich gilt im Fall von exakten
Daten und dem klassischen Konfidenzbereich
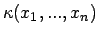 :
:
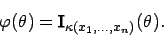
Allgemein gilt
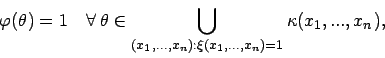
d.h die Indikatorfunktion der Vereinigung auf der rechten Seite ist immer unterhalb der charakterisierenden Funktion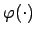 des unscharfen Konfidenzintervalles.
Mit der Abkürzung
des unscharfen Konfidenzintervalles.
Mit der Abkürzung
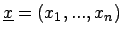 kann man schreiben
kann man schreiben
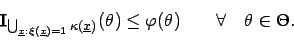
Das erkennt man am einfachsten durch:
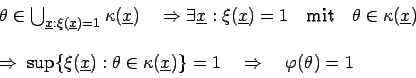
- Beispiel 2.1:
- Ein unscharfer Konfidenzbereich für den Parameter
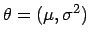 einer Normalverteilung basierend auf unscharfen Daten ist in Abbildung
einer Normalverteilung basierend auf unscharfen Daten ist in Abbildung ![[*]](cross_ref_motif.gif) zu sehen.
zu sehen.
Konfidenzbereiche für geraffte Parameter bei unscharfen Daten
Für Funktionen
![]() des Parameters
des Parameters ![]() eines stochastischen Modells
eines stochastischen Modells
![]() mit
gerafftem Parameterraum
mit
gerafftem Parameterraum
![]() kann das Konzept der Konfidenzbereiche ebenfalls verallgemeinert werden.
kann das Konzept der Konfidenzbereiche ebenfalls verallgemeinert werden.
- Definition 2.2:
- Ist
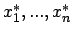 eine unscharfe Stichprobe,
dessen unscharfes kombiniertes Stichprobenelement
eine unscharfe Stichprobe,
dessen unscharfes kombiniertes Stichprobenelement
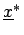 die
vektorcharakterisierende Funktion
die
vektorcharakterisierende Funktion
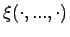 aufweist, so
ist für eine Konfidenzfunktion
aufweist, so
ist für eine Konfidenzfunktion
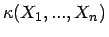 für geraffte
Parameter
für geraffte
Parameter
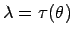 ein verallgemeinerter Konfidenzbereich
für
ein verallgemeinerter Konfidenzbereich
für
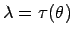 eine unscharfe Teilmenge
eine unscharfe Teilmenge 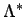 von
von 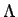 , deren charakterisierende Funktion
, deren charakterisierende Funktion 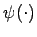 gegeben ist durch
gegeben ist durch
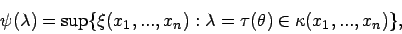
wobei für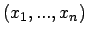 alle Werte innerhalb des Stichprobenraumes
berücksichtigt werden müssen.
alle Werte innerhalb des Stichprobenraumes
berücksichtigt werden müssen. - Bemerkung:
- Für geraffte Parameter
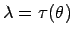 gilt ebenfalls
gilt ebenfalls
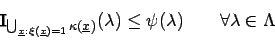
mit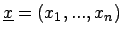 und
und
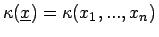 .
. - Beispiel 2.2:
- Ist
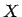 eine normalverteilte, stochastische Größe und
eine normalverteilte, stochastische Größe und
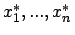 eine unscharfe Stichprobe von
eine unscharfe Stichprobe von 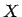 , so soll ein verallgemeinertes Konfidenzintervall
für
, so soll ein verallgemeinertes Konfidenzintervall
für
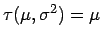 berechnet werden.
berechnet werden.
Ist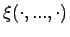 die vektorcharakterisierende Funktion des
unscharfen kombinierten Stichprobenelements, so wird die charakterisierende
Funktion
die vektorcharakterisierende Funktion des
unscharfen kombinierten Stichprobenelements, so wird die charakterisierende
Funktion 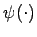 des verallgemeinerten Konfidenzintervalles für
des verallgemeinerten Konfidenzintervalles für
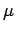 mittels eines klassischen Konfidenzintervalles
mittels eines klassischen Konfidenzintervalles
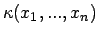 für
für 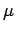 basierend auf den exakten Daten
basierend auf den exakten Daten
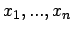 berechnet.
Für eine Überdeckungswahrscheinlichkeit von
berechnet.
Für eine Überdeckungswahrscheinlichkeit von 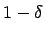 gilt
gilt
![\begin{displaymath}
\kappa (x_{1},...,x_{n})=[\overline{x}_{n}-\frac{s_{n}}{\sqr...
...}_{n}+\frac{s_{n}}{\sqrt{n}}\cdot t_{n-1;1-\frac{\delta }{2}}].\end{displaymath}](img106.gif)
Die charakterisierende Funktion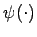 des verallgemeinerten unscharfen
Konfidenzintervalles basierend auf den unscharfen Daten ist gegeben durch
des verallgemeinerten unscharfen
Konfidenzintervalles basierend auf den unscharfen Daten ist gegeben durch
![\begin{displaymath}
\psi (\mu )=\sup \{\xi (\underline{x}):\mu \in [\overline{x}...
..._{n}+\frac{s_{n}}{\sqrt{n}}\cdot t_{n-1;1-\frac{\delta }{2}}]\}\end{displaymath}](img107.gif)
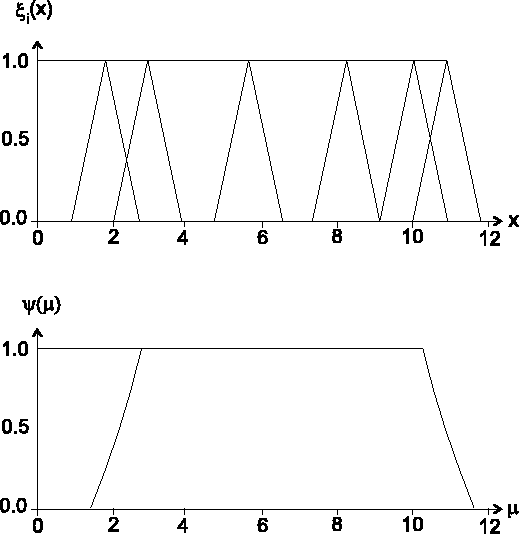
In Abbildung![[*]](cross_ref_motif.gif) ist eine unscharfe Stichprobe einer
Normalverteilung und das entsprechende unscharfe Konfidenzintervall für
ist eine unscharfe Stichprobe einer
Normalverteilung und das entsprechende unscharfe Konfidenzintervall für 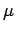 dargestellt.
dargestellt.
Nichtparametrische Schätzung
Die wichtigste nichtparametrische Schätzung der Verteilungsfunktion einer eindimensionalen
stochastischen Größe ![]() basierend auf einer Stichprobe
basierend auf einer Stichprobe
![]() ist die empirische Verteilungsfunktion
ist die empirische Verteilungsfunktion
![]() gegeben durch:
gegeben durch:
![\begin{displaymath}
\hat{F}_{n}(x)=\frac{1}{n}\sum _{i=1}^{n}I_{(-\infty ,x]}(X_{i})\qquad \forall x\in \mathbb {R}\end{displaymath}](img110.gif)
Für unscharfe Beobachtungen
![]() von
von ![]() sind
mehrere Verallgemeinerungen möglich.
sind
mehrere Verallgemeinerungen möglich.
Geglättete empirische Verteilungsfunktion
Die klassische empirische Verteilungsfunktion ist eine Treppenfunktion. Um stetige Verteilungen zu schätzen, wäre eine stetige Schätzung der Verteilungsfunktion von Vorteil.
Für unscharfe Daten
![]() mit charakterisierenden Funktionen
mit charakterisierenden Funktionen
![]() ist eine stetige Schätzung der
Verteilung gegeben durch
ist eine stetige Schätzung der
Verteilung gegeben durch
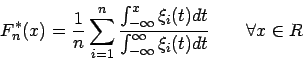
Die geglättete empirische Verteilungsfunktion ist nur dann definiert, wenn alle Beobachtungen unscharf sind.
In Abbildung ![[*]](cross_ref_motif.gif) ist eine unscharfe
Stichprobe und die entsprechende Schätzung
ist eine unscharfe
Stichprobe und die entsprechende Schätzung
![]() dargestellt.
dargestellt.
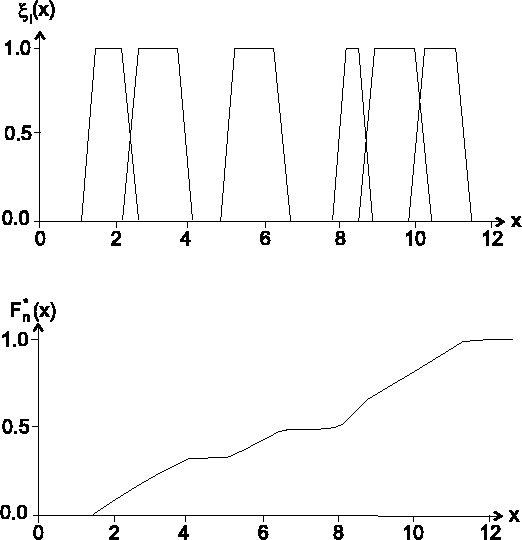
|
Intervallwertige empirische Verteilungsfunktion
Für Intervalldaten ist eine verallgemeinerte empirische Verteilungsfunktion gegeben durch
Für allgemeine unscharfe Beobachtungen
![]() mit charakterisierenden
Funktionen
mit charakterisierenden
Funktionen
![]() sind die Funktionen
sind die Funktionen
![]() und
und
![]() auf folgende
Weise definiert:
auf folgende
Weise definiert:
Im Fall von paarweise disjunkten Trägern
![]() können die charakterisierenden Funktionen der Größe nach geordnet und als
können die charakterisierenden Funktionen der Größe nach geordnet und als
![]() angeschrieben werden.
angeschrieben werden.
Im Intervall
![]() sind die
Funktionen
sind die
Funktionen
![]() und
und
![]() gegeben durch
gegeben durch
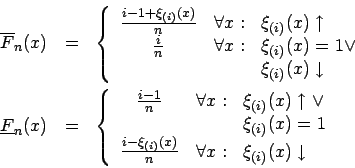
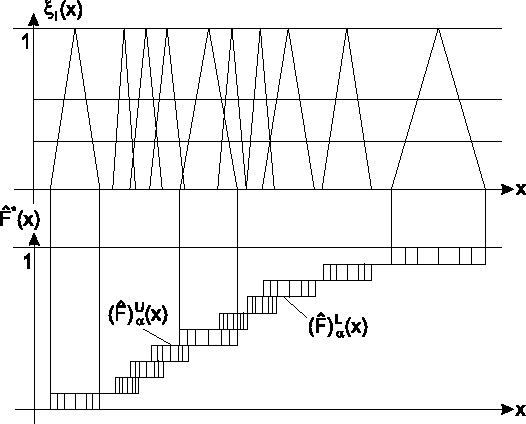
Abbildung ![[*]](cross_ref_motif.gif) zeigt einen
Ausschnitt dieser beiden Funktionen im Intervall
zeigt einen
Ausschnitt dieser beiden Funktionen im Intervall
![]() einer Beobachtung sowie für eine Stichprobe mit vier unscharfen Beobachtungen
die gesamte intervallwertige empirische Verteilungsfunktion
einer Beobachtung sowie für eine Stichprobe mit vier unscharfen Beobachtungen
die gesamte intervallwertige empirische Verteilungsfunktion
![]() .
.
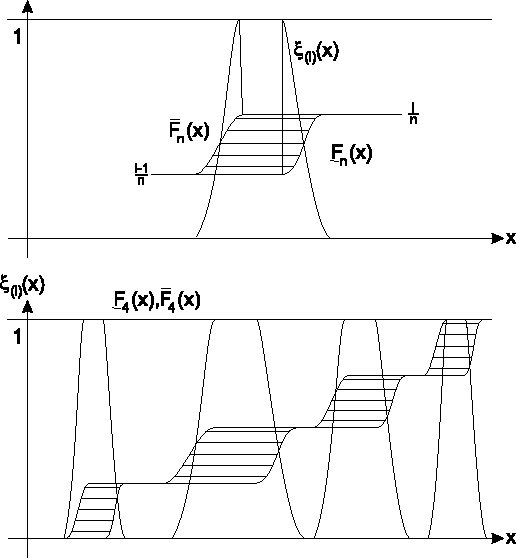
|
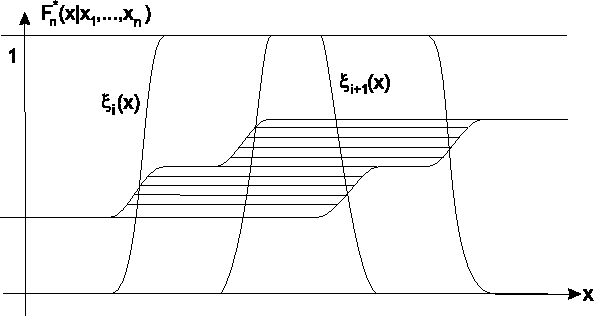
- Bemerkung:
- Für unscharfen Daten mit sich überschneidenden Trägern wird eine
Überlagerung der Funktionen
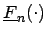 und
und
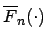 erzeugt. Ein Beispiel dafür zeigt Abbildung
erzeugt. Ein Beispiel dafür zeigt Abbildung ![[*]](cross_ref_motif.gif) .
.
Anwendung der Fortpflanzung der Unschärfe
Für eine Stichprobe von ![]() unscharfen Beobachtungen einer eindimensionalen
stochastischen Größe
unscharfen Beobachtungen einer eindimensionalen
stochastischen Größe ![]() ist
ist
![]() die vektorcharakterisierende
Funktion des unscharfen kombinierten Stichprobenelements.
die vektorcharakterisierende
Funktion des unscharfen kombinierten Stichprobenelements.
Die klassische empirische Verteilungsfunktion
![]() , gegeben
durch
, gegeben
durch
![\begin{displaymath}
\hat{F}_{n}(x)=\frac{1}{n}\sum _{i=1}^{n}I_{(-\infty ,x]}(x_{i})\end{displaymath}](img133.gif)
kann nicht direkt verwendet werden, um eine verallgemeinerte empirische Verteilungsfunktion zu konstruieren, da sie nicht stetig ist.
Eine Verallgemeinerung ist aber mittels der invertierten empirischen Verteilungsfunktion möglich:
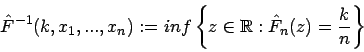
Diese Funktion ist stetig in den Beobachtungen
![]() . Daher
erhält man für die unscharfen Daten
. Daher
erhält man für die unscharfen Daten
![]() die Funktion
die Funktion
Die verallgemeinerte invertierte unscharfe empirische Verteilungsfunktion ist
definiert durch ihre unscharfen Werte
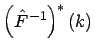 mit der charakterisierenden Funktion
mit der charakterisierenden Funktion
![]() gegeben durch
gegeben durch
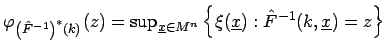 mit
mit
Die ![]() -Niveaukurven dieser verallgemeinerten empirischen Verteilungsfunktion
sind gegeben durch
-Niveaukurven dieser verallgemeinerten empirischen Verteilungsfunktion
sind gegeben durch
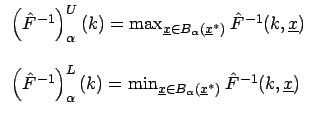 mit
mit
- Bemerkung:
- Falls die Minimum-Kombinationsregel verwendet wird, kann die verallgemeinerte
korrespondierende empirische Verteilungsfunktion durch ihre oberen und unteren
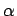 -Niveaukurven
-Niveaukurven
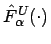 und
und
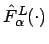 dargestellt werden:
dargestellt werden:
![\begin{displaymath}
\hat{F}_{\alpha }^{U}(z)=\frac{1}{n}\sum _{i=1}^{n}I_{(-\infty ,z]}\left( \underline{B}_{\alpha }(x_{i}^{*})\right) \end{displaymath}](img144.gif)
![\begin{displaymath}
\hat{F}_{\alpha }^{L}(z)=\frac{1}{n}\sum _{i=1}^{n}I_{(-\infty ,z]}\left( \overline{B}_{\alpha }(x_{i}^{*})\right) \end{displaymath}](img145.gif)
Dabei bezeichnet![\( B_{\alpha }(x_{i}^{*})=\left[ \underline{B}_{\alpha }(x_{i}^{*}),\overline{B}_{\alpha }(x_{i}^{*})\right] \)](img146.gif) die
die 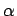 -Schnitte der Beobachtungen
-Schnitte der Beobachtungen 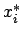 . Ein Beispiel
zeigt Abbildung
. Ein Beispiel
zeigt Abbildung ![[*]](cross_ref_motif.gif) .
.
Graphische Verallgemeinerung der empirischen Verteilungsfunktion
Für unscharfe Beobachtungen
![]() einer eindimensionalen
stochastischen Größe
einer eindimensionalen
stochastischen Größe ![]() kann eine graphische Verallgemeinerung der empirischen
Verteilungsfunktion auf folgende Weise erstellt werden.
kann eine graphische Verallgemeinerung der empirischen
Verteilungsfunktion auf folgende Weise erstellt werden.
Sind
![]() die charakterisierenden Funktionen
der unscharfen Beobachtungen
die charakterisierenden Funktionen
der unscharfen Beobachtungen
![]() , so kann durch Ordnen
der Funktionen
, so kann durch Ordnen
der Funktionen
![]() nach den linken
Grenze ihrer Träger
nach den linken
Grenze ihrer Träger
![]() und Bezeichnung der
geordneten Menge mit
und Bezeichnung der
geordneten Menge mit
![]() eine Verallgemeinerung
der klassischen empirischen Verteilungsfunktion
eine Verallgemeinerung
der klassischen empirischen Verteilungsfunktion
![]() erstellt
werden. Abbildung
erstellt
werden. Abbildung ![[*]](cross_ref_motif.gif) stellt dies dar.
stellt dies dar.
- Bemerkung:
- Im Fall, dass alle charakterisierenden Funktionen
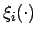 die gleiche Form aufweisen, d.h. sie können als Transformation untereinander
aufgefaßt werden, besitzen die
die gleiche Form aufweisen, d.h. sie können als Transformation untereinander
aufgefaßt werden, besitzen die 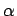 -Niveaukurven der graphischen Verallgemeinerung
-Niveaukurven der graphischen Verallgemeinerung
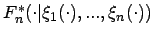 die Form von
klassischen empirischen Verteilungsfunktionen.
die Form von
klassischen empirischen Verteilungsfunktionen.
Empirischer Korrelationskoeffizient für unscharfe Beobachtungen
Der klassische empirische Korrelationskoeffizient ![]() für genaue
Beobachtungen
für genaue
Beobachtungen
![]() , gegeben durch
, gegeben durch
![\begin{displaymath}
r_{x,y}=\frac{\sum _{i=1}^{n}(x_{i}-\overline{x}_{n})(y_{i}-...
...t \left[ \sum _{i=1}^{n}(y_{i}-\overline{y}_{n})^{2}\right] }},\end{displaymath}](img157.gif)
kann für unscharfe Daten auf folgende Weise verallgemeinert werden:
Insgesamt ![]() unscharfe zweidimensionale Beobachtungen
unscharfe zweidimensionale Beobachtungen
![]() mit korrespondierenden charakterisierenden Funktionen
mit korrespondierenden charakterisierenden Funktionen
werden zu einem unscharfen Element des Stichprobenraumes
![]() zusammengefaßt. Die vektorcharakterisierende Funktion dieses Elements ist gegeben
durch
zusammengefaßt. Die vektorcharakterisierende Funktion dieses Elements ist gegeben
durch
und kann durch eine entsprechende Kombination der charakterisierenden Funktionen
![]() ermittelt werden.
ermittelt werden.
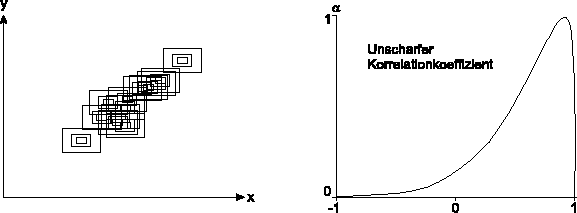
Mögliche Kombinationen sind
und
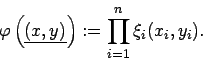
Der verallgemeinerte empirische Korrelationskoeffizient ist dann die unscharfe
Zahl ![]() , bezeichnet als unscharfer Korrelationskoeffizient,
basierend auf einer unscharfen Stichprobe
, bezeichnet als unscharfer Korrelationskoeffizient,
basierend auf einer unscharfen Stichprobe
![]() ,
definiert durch seine charakterisierende Funktion
,
definiert durch seine charakterisierende Funktion
![]()
|
Ergänzende Beispiele
- Beispiel 3.1:
- Es ist der Unterschied zwischen der geglätteten empirischen Verteilungsfunktion
und der Summenkurve zu erklären.
Dazu betrachtet man zuerst die Definition der Summenkurve:
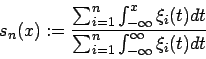
Diese summiert die Flächen unterhalb der charakterisierenden Funktionen bis zum Punkt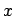 auf und dividiert dann durch die Gesamtfläche unterhalb aller
charakterisierenden Funktionen. Das heißt, es wird die Gesamtfläche unterhalb
aller charakterisierenden Funktionen zur Normierung herangezogen.
auf und dividiert dann durch die Gesamtfläche unterhalb aller
charakterisierenden Funktionen. Das heißt, es wird die Gesamtfläche unterhalb
aller charakterisierenden Funktionen zur Normierung herangezogen.
Nun betrachtet man die Definition der geglätteten empirischen Verteilungsfunktion:
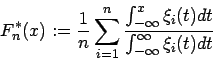
Diese normiert die Fläche unter jeder einzelnen charakterisierenden Funktion auf eins. Deshalb muß man abschließend noch durch die Anzahl der Beobachtungen dividieren. Dadurch erklärt sich auch, warum die geglättete empirische Verteilungsfunktion nur für unscharfe Werte definiert ist. Wäre eine Beobachtung exakt, würde es zu einer Division durch Null kommen.
Abbildung![[*]](cross_ref_motif.gif) zeigt die Unterschiede auf.
zeigt die Unterschiede auf. -
Abbildung: Vergleich zwischen geglätteter empirischer Verteilungsfunktion und Summenkurve: Der Anstieg der Summenkurve (dicke Linie) bei jeder Beobachtung ist abhängig von der Fläche unterhalb der charakterisierenden Funktion dieser Beobachtung. Je größer, d.h. je unschärfer diese ist, desto größer ist der Anstieg, der durch diese Beobachtung verursacht wird. Die geglättete empirische Verteilungsfunktion hingegen steigt bei jeder Beobachtung um 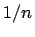 an.
an. 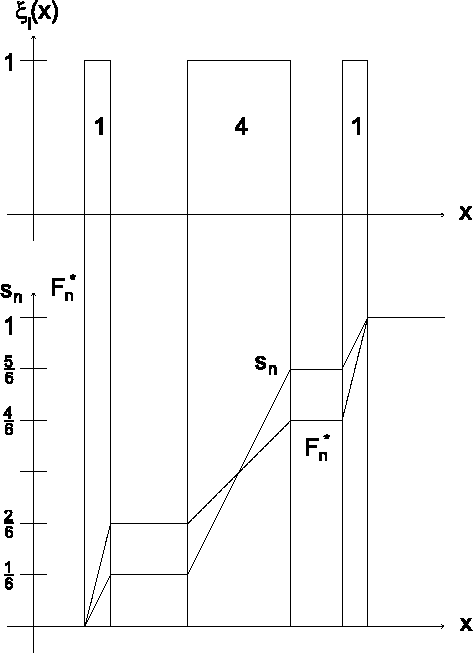
- Beispiel 3.2:
- Es ist der Zusammenhang zwischen der verallgemeinerten empirischen
Verteilungsfunktion für Intervalldaten und der intervallwertigen empirischen
Verteilungsfunktion zu zeigen.
Die intervallwertige empirische Verteilungsfunktion ist definiert als
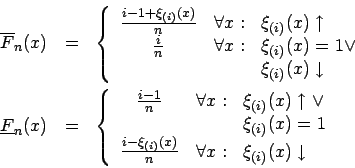
Da bei Intervalldaten die charakterisierende Funktion nur die Werte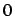 oder
oder 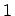 annehmen kann, läßt sich der Ausdruck vereinfachen zu:
annehmen kann, läßt sich der Ausdruck vereinfachen zu:
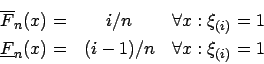
Dies entspricht der empirischen Verteilungsfunktion für Intervalldaten.
Statistische Tests bei unscharfen Daten
Bei klassischen Signifikanztests basierend auf exakten Beobachtungen
![]() einer stochastischen Größe
einer stochastischen Größe
![]() und Beobachtungsraum
und Beobachtungsraum
![]() , ist die Entscheidung abhängig vom Wert einer Teststatistik
, ist die Entscheidung abhängig vom Wert einer Teststatistik
![]() basierend auf einer Stichprobe
basierend auf einer Stichprobe
![]() von
von ![]() .
.
Für unscharfe Beobachtungen
![]() mit unscharfem kombinierten
Stichprobenelement
mit unscharfem kombinierten
Stichprobenelement
![]() und entsprechender vektorcharakterisierender
Funktion
und entsprechender vektorcharakterisierender
Funktion
![]() wird der Wert der Teststatistik unscharf.
Die charakterisierende Funktion
wird der Wert der Teststatistik unscharf.
Die charakterisierende Funktion ![]() dieses unscharfen Wertes
dieses unscharfen Wertes
![]() der Teststatistik
der Teststatistik
![]() ist gegeben durch
ist gegeben durch
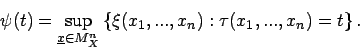
- Beispiel 4.1:
- Für eine Stichprobe
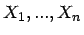 einer normalverteilten
stochastischen Größe
einer normalverteilten
stochastischen Größe
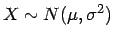 ist eine Teststatistik
für die Hypothese
ist eine Teststatistik
für die Hypothese
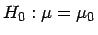 gegeben durch
gegeben durch
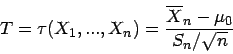
mit Annahmeraum A und Wahrscheinlichkeit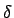 für einen Fehler 1.
Art
für einen Fehler 1.
Art
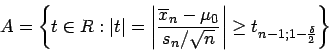
wobei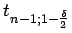 das
das
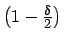 -Fraktile
der t-Verteilung mit
-Fraktile
der t-Verteilung mit 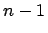 Freiheitsgraden darstellt.
Freiheitsgraden darstellt.
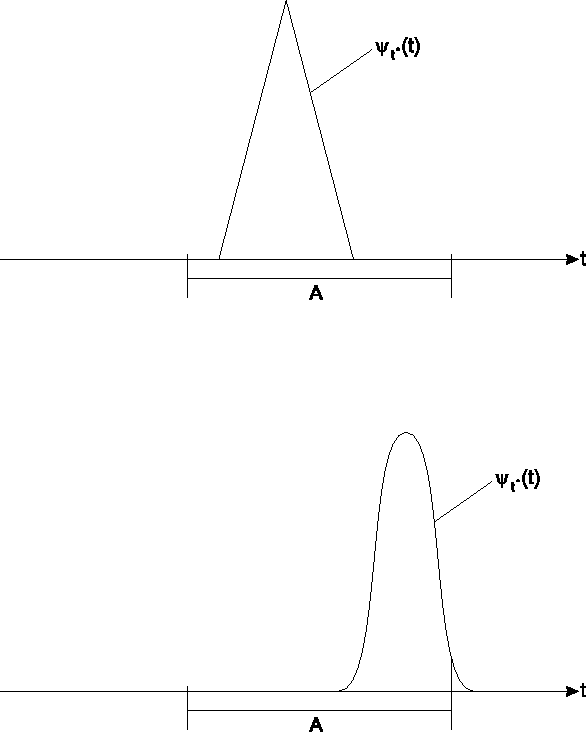
In Abbildung ![[*]](cross_ref_motif.gif) sind zwei mögliche charakterisierende
Funktionen des unscharfen Wertes
sind zwei mögliche charakterisierende
Funktionen des unscharfen Wertes ![]() dargestellt.
dargestellt.
|
Falls der Träger von ![]() eine Teilmenge von
eine Teilmenge von ![]() oder eine Teilmenge
von
oder eine Teilmenge
von ![]() ist, dann ist eine Entscheidung über Annahme oder Verwerfung
genau wie für exakte Daten möglich.
ist, dann ist eine Entscheidung über Annahme oder Verwerfung
genau wie für exakte Daten möglich.
Für den Fall, dass der Träger von ![]() nichtleere Schnittmengen mit
nichtleere Schnittmengen mit
![]() und
und ![]() hat, ist eine einfache Entscheidung nicht möglich.
In diesem Fall sind z.B. mehr Beobachtungen notwendig.
hat, ist eine einfache Entscheidung nicht möglich.
In diesem Fall sind z.B. mehr Beobachtungen notwendig.
Literatur
- 1
- R. Viertl: Statistical Methods for Non-Precise Data, CRC Press, Boca Raton, Florida, 1996.
Über dieses Dokument ...
Seminararbeit aus Angewandter StatistikKlassische schließende Statistik für unscharfe Daten
This document was generated using the LaTeX2HTML translator Version 99.1 release (March 30, 1999)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -split 0 -local_icons -no_footnode -no_navigation -html_version 4.0 -dir ./html FuzzySeminar.tex
The translation was initiated by on 2000-01-21
Fußnoten
- ... Supremum
![[*]](foot_motif.gif)
- In dieser Arbeit wird zur Vereinfachung davon ausgegangen, dass das Supremum
der leeren Menge gleich
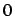 ist. Um formal korrekte Ausdrücke zu erhalten,
muß ein Ausdruck der Form
ist. Um formal korrekte Ausdrücke zu erhalten,
muß ein Ausdruck der Form
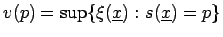 umgeschrieben werden als
umgeschrieben werden als