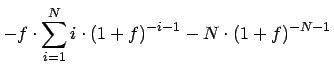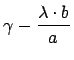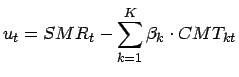Download PDF Download Excel files
Bewertung von SMR-Produkten
Martin Vonwald
November 1999
Vorwort
An dieser Stelle möchte ich mich bei meinem Diplomarbeitsbetreuer Prof. Stefan Pichler bedanken, der mit seinen wertvollen Anregungen entscheidend zum guten Gelingen dieser Arbeit beigetragen hat. Ein weiteres Dankeschön geht an meine Korrekturleser Michaela Escuyer und Karl Selitsch, welche dieser Arbeit den letzten Schliff gegeben haben. Nicht zuletzt gebührt den Mitgliedern der LYX-Usergroup und natürlich den LYX-Entwickler mein Dank, die es mir ermöglichten diese Arbeit in der vorliegenden Form umzusetzen.
Inhalt
Einführung
Motivation
Eine der bedeutsamsten Gruppen von Zahlungsströmen im Kredit- und Anleihenbereich
sowie auf den stark wachsenden Swapmärkten ist die Gruppe der Floater. Dies
sind Zahlungsströme, deren Kupon im Gegensatz zu Anleihen an einen bestimmten
variablen Zinssatz gebunden sind. Trotz der großen Bedeutung von Floatern
existiert jedoch relativ wenig Literatur zu diesem Thema (vgl. [![[*]](cross_ref_motif.gif) ],
[
],
[![[*]](cross_ref_motif.gif) ]).
]).
Eine speziell für den österreichischen Kapitalmarkt wichtige Gruppe von Finanztitel
sind sog. ,,SMR-Floater``. Dies sind Floater mit Bindung an einen Kapitalmarktzinssatz
mit variabler Laufzeit, einer sog. Sekundärmarktrendite (kurz: SMR). Eine SMR
kann im wesentlichen als gewichteter Durchschnitt von Endfälligkeitsrenditen
von Anleihen eines bestimmten Marktsegments betrachtet werden (vgl. Abschnitt
![[*]](cross_ref_motif.gif) ), wobei jedoch zu beachten ist, dass sich
die Zusammensetzung des Marktsegments häufig ändern kann, da immer wieder Anleihen
auslaufen oder neue Anleihen emmitiert werden. Vor allem diese Eigenschaft macht
eine Bewertung von SMR-abhängigen Produkten problematisch.
), wobei jedoch zu beachten ist, dass sich
die Zusammensetzung des Marktsegments häufig ändern kann, da immer wieder Anleihen
auslaufen oder neue Anleihen emmitiert werden. Vor allem diese Eigenschaft macht
eine Bewertung von SMR-abhängigen Produkten problematisch.
Um SMR-Produkte bewerten zu können, muss die SMR entsprechend modelliert werden. Grundsätzlich gibt es hierzu zwei einfache Ansätze, die jedoch beide mehr oder weniger gravierende Nachteile aufweisen:
- Eine endogene Modellierung der SMR basierend auf einem Zinsstrukturmodell.
Dabei trifft man die Annahme, dass bereits zum Bewertungszeitpunkt alle zukünftigen Zahlungsströme und Umlaufvolumina aller Anleihen bekannt sind. Dies ist jedoch ausgesprochen problematisch, wenn man bedenkt, dass jederzeit neue Anleihen emittiert werden können und diese dann in die Berechnung der SMR eingehen.
Weiters nimmt man bei diesem Ansatz ebenfalls an, dass die Preise aller Anleihen ihren arbitragefreien Werten entsprechen. Abgesehen von Bid-Ask-Spreads, die dazu führen, dass die Marktpreise nicht exakt den theoretischen Preisen entsprechen, ist der österreichische Kapitalmarkt unvollständig. Dies führt dazu, dass abweichende Bewertungen nicht arbitriert werden können.
- Modellierung der SMR als exogenen stochastischen Prozess.
Der gravierendste Nachteil dieses Ansatzes liegt darin, dass man entweder einen sehr einfachen Prozess verwendet und dabei ausgesprochen unrealistische Annahmen treffen muss (z.B. Unkorreliertheit zwischen SMR und Zinsstruktur), oder aber man bedient sich eines aufwendigeren Prozesses und hat dann Probleme bei der Prozessspezifikation und der Parameterschätzung zu lösen. Ein weiterer Nachteil liegt darin, dass der überwiegende Teil der Bewertung von Parametern abhängt, die an Preise von SMR-abhängigen Instrumenten kalibriert werden müssen, wodurch sich eine relativ hohe Ungenauigkeit ergeben kann.
![[*]](cross_ref_motif.gif) ] vorgestellt
wurde, teilt in der Modellierung die SMR in einen endogenen Teil und einen exogenen
Fehlerprozess auf. Im endogenen Teil werden Änderungen der SMR durch Änderungen
von mehreren Constant Maturity Treasury Rates (CMT) beschrieben. Eine CMT ist
eine Par-Coupon Yield, welche aus den Preisen von Staatsanleihen mit standardisierten
Laufzeiten ermitteln wird (vgl. [
] vorgestellt
wurde, teilt in der Modellierung die SMR in einen endogenen Teil und einen exogenen
Fehlerprozess auf. Im endogenen Teil werden Änderungen der SMR durch Änderungen
von mehreren Constant Maturity Treasury Rates (CMT) beschrieben. Eine CMT ist
eine Par-Coupon Yield, welche aus den Preisen von Staatsanleihen mit standardisierten
Laufzeiten ermitteln wird (vgl. [![[*]](cross_ref_motif.gif) ] und Abschnitt
] und Abschnitt
![[*]](cross_ref_motif.gif) ). Der exogene Fehlerprozess hingegen beschreibt die Abweichungen
der modellmäßigen SMR von der realen SMR. Im Gegensatz zur Modellierung der
SMR als exogenen stochastischen Prozess ist bei der Bewertung nur ein sehr kleiner
Teil des Barwertes von zu kalibrierenden Parametern abhängig.
). Der exogene Fehlerprozess hingegen beschreibt die Abweichungen
der modellmäßigen SMR von der realen SMR. Im Gegensatz zur Modellierung der
SMR als exogenen stochastischen Prozess ist bei der Bewertung nur ein sehr kleiner
Teil des Barwertes von zu kalibrierenden Parametern abhängig.
Der Vorteil dieses Ansatzes ist es, die einzelnen Kuponzahlungen in einen auf herkömmliche Weise hedgebaren Teil und einen Fehlerteil zu trennen. Somit wäre es möglich, große Teile von SMR-Produkten durch Zerobonds nachzubilden. Die verbleibenden relativ kleinen Abweichungen werden durch den Fehlerprozess beschrieben und müssten durch andere SMR-Produkte gehedgt werden.
Genau diesem Ansatz widmet sich auch diese Arbeit. Zu Beginn wird eine zusammenfassende Darstellung des Bewertungsmodells gegeben und anschließend wird eine Softwareapplikation vorgestellt, welche auf Basis dieses Modells entwickelt wurde. Da es sich hierbei um die erstmalige Umsetzung dieses Modells in Form eines konkreten Bewertungstool handelt, wurde auch Bedacht auf eine sehr genaue Dokumentation gelegt. Gerade auch die vielfältigen Anwendungsmöglichkeiten eines solchen Tools, wie z.B.
- Bewertung von SMR-abhängigen Anleihen und Krediten,
- Bewertung von SMR-abhängigen Leasing- und Mietverträgen oder
- Risikobeurteilung von SMR-abhängigen Kapitalmarktfloatern zwecks Gesamtbanksteuerung
- Ein dialoggesteuerter Assistent führt den Anwender durch den Modellkalibrierungsvorgang und den darauffolgenden Bewertungsvorgang.
- Mehrere Excel-Makros erlauben die simultane Kalibrierung verschiedener Modelle und die Bewertung mehrerer SMR-Floater innerhalb einer Excel-Arbeitsmappe.
Im ersten Kapitel werden die Begriffe SMR und SMR-Floater vorgestellt und erläutert.
Außerdem wird noch ein kurzer Literaturüberblick gegeben. In Kapitel ![[*]](cross_ref_motif.gif) wird das verwendete Bewertungsmodell im Detail vorgestellt. Kapitel
wird das verwendete Bewertungsmodell im Detail vorgestellt. Kapitel ![[*]](cross_ref_motif.gif) widmet sich dann dem erstellten Bewertungstool. Es werden die zwei unabhängigen
Programmmodule vorgestellt und deren Bedienung erläutert. Der Aufbau der einzelnen
Programmteile wird in Kapitel
widmet sich dann dem erstellten Bewertungstool. Es werden die zwei unabhängigen
Programmmodule vorgestellt und deren Bedienung erläutert. Der Aufbau der einzelnen
Programmteile wird in Kapitel ![[*]](cross_ref_motif.gif) beschrieben. Außerdem
wird anhand eines konkreten Zahlenbeispiels der genaue Ablauf des Kalibrierungs-
und Bewertungsvorganges gezeigt. Abschließend wird dann in Kapitel
beschrieben. Außerdem
wird anhand eines konkreten Zahlenbeispiels der genaue Ablauf des Kalibrierungs-
und Bewertungsvorganges gezeigt. Abschließend wird dann in Kapitel ![[*]](cross_ref_motif.gif) auf die möglichen Dateiformate eingegangen, in welchen die notwendigen Daten
(z.B. SMR- oder Spotrates-Zeitreihen) vorliegen können.
auf die möglichen Dateiformate eingegangen, in welchen die notwendigen Daten
(z.B. SMR- oder Spotrates-Zeitreihen) vorliegen können.
SMR und davon abhängige Finanzinstrumente
Sekundärmarktrendite
Eine Sekundärmarktrendite (SMR) ist ein Kapitalmarktzinssatz mit variabler Laufzeit,
wobei dieser als gewichteter Durchschnitt von Endfälligkeitsrenditen von bestimmten
Gruppen von Anleihen betrachtet werden kann. Die Berechnung der SMR ist von
folgenden Punkten abhängig (vgl. [![[*]](cross_ref_motif.gif) ]):
]):
- Welche Gruppe von Anleihen wird verwendet?
Neben der Währung und der Verzinsungsform (variabel-/festverzinst) spielt hierbei auch die Bonitätsklasse der Schuldner eine Rolle. Außerdem kann eine Unterscheidung auch nach Restlaufzeit und eventuell vorhandenen Kündigungsrechten erfolgen.
- Wie wird die Endfälligkeitsrendite berechnet?
Eine weit verbreitete Methode zur Bestimmung der Endfälligkeitsrendite ist die Verwendung der Effektivverzinsung. Diese beruht auf der Annahme, dass alle innerhalb der Laufzeit anfallenden Zahlungen zu einem bestimmten fixen Zinssatz wiederveranlagt werden können.
Die österreichische Kontrollbank hingegen verwendet zur Berechnung der SMR die sog. ,,reale`` Rendite, die einem fix vorgegebenen Zinssatz entspricht (7,5% oder 8%).
- Wie werden die Endfälligkeitsrenditen gewichtet?
Neben der Gewichtung nach Börsenumsatz (Umsatzgewichtung) kommt auch eine Gewichtung nach dem ausstehenden Nominale (Umlaufgewichtung) zur Anwendung.
- Anleihengruppen
Die Anleihen werden in 15 Gruppen aus festverzinsten Emmisionen, 10 Gruppen aus Kapitalmarktfloatern und 7 Gruppen aus Geldmarktfloatern eingeteilt.
- Restlaufzeit
Neben einer SMR für alle Restlaufzeiten wird auch eine SMR für Restlaufzeiten größer als ein Jahr und eine SMR für Restlaufzeiten größer als drei Jahre berechnet.
![[*]](cross_ref_motif.gif) ]):
]):
- Berechnung der ,,realen`` Renditen
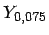 und
und 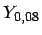 für
jede Anleihe in der betrachteten Gruppe:
für
jede Anleihe in der betrachteten Gruppe:
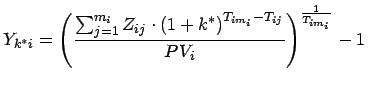
(1)
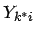
Reale Rendite für Anleihe 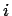 und Wiederveranlagungssatz
und Wiederveranlagungssatz 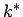 mit
mit
#MATH9# bzw. 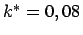
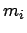
Anzahl der Zahlungen der Anleihe 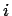
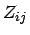
Zahlungen der Anleihe 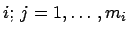
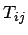
Zahlungszeitpunkte der Anleihe 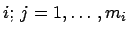
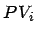
Marktwert der Anleihe 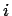 (entspricht dem Börsenkurs inklusive Stückzinsen).
Ist der Börsenkurs nicht beobachtbar, wird der letzte beobachtete Börsenkurs
herangezogen.
(entspricht dem Börsenkurs inklusive Stückzinsen).
Ist der Börsenkurs nicht beobachtbar, wird der letzte beobachtete Börsenkurs
herangezogen.
- Umlaufgewichtung über die gesamte Gruppe:
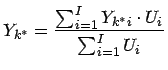
(2)
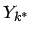
Umlaufgewichteter Durchschnitt der ,,realen`` Renditen mit Wiederveranlagungssatz 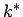 innerhalb der Gruppe.
innerhalb der Gruppe.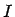
Anzahl der Anleihen innerhalb der betrachteten Gruppe. 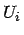
Noch nicht getilgtes Nominale der Anleihe 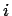 .
.
- Berechnung der SMR:
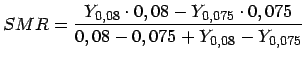
(3)
SMR-Floater
Kapitalmarktfloater mit Bindung an eine SMR bezeichnet man als SMR-Floater. Die wichtigsten Unterscheidungsmerkmale werden im folgenden angeführt:
- Welche SMR dient als Referenzzinssatz?
- Wann sind die Anpassungszeitpunkte und welche Regeln werden verwendet?
Falls beides bei Vetragsabschluss genau festgelegt wird, spricht man von einer fixen Zinsbindung, anderenfalls von einer nicht fixen Zinsbindung.
- Wann wird die Höhe der Kuponzahlung festgelegt?
Erfolgt die Anpassung am Anfang der Kuponperiode spricht man von einer regulären Zinsanpassung. Bei einer Anpassung am Ende der Kuponperiode nennt man dies in-arrears Zinsanpassung. Eine weitere Möglichkeit ist die Durchschnittsanpassung. Diese liegt dann vor, wenn die Kuponzahlung von der durchschnittlichen Höhe des Referenzzinssatzes während einer Referenzperiode abhängig ist.
- Wie wird die Höhe der Kuponzahlung ermittelt?
Wenn man unterstellt, dass die Höhe der Kuponzahlung als Funktion des Referenzzinssatzes darzustellen ist, kann man u.a. zwischen folgenden Anpassungsfunktionen unterscheiden:
- Perfekt indiziert
Die Verzinsung entspricht dem Referenzzinssatz.
- Margin
Entspricht einem Auf- bzw. Abschlag auf den Referenzzinssatz.
- Rundung
Hierbei wird der Referenzzinssatz auf einen bestimmten Wert gerundet.
- Zinsober-/untergrenze (Cap/Floor)
Es wird festgelegt, dass die Verzinsung einen bestimmten Wert nicht über- bzw. unterschreiten darf.
Literaturüberblick
Eine der ersten Arbeiten die sich mit der Bewertung von Geldmarktfloater befasst
hat, wurde von Ramaswamy und Sundaresan [![[*]](cross_ref_motif.gif) ]
erstellt. Ausgehend von einem Einfaktor-Modell wurde ein allgemeiner Bewertungsansatz
für Geldmarktfloater (Durchschnitts-Zinsanpassung) entworfen. Unter Anwendung
des Forward Measure wurde von Li und Raghavan [
]
erstellt. Ausgehend von einem Einfaktor-Modell wurde ein allgemeiner Bewertungsansatz
für Geldmarktfloater (Durchschnitts-Zinsanpassung) entworfen. Unter Anwendung
des Forward Measure wurde von Li und Raghavan [![[*]](cross_ref_motif.gif) ]
ein Modell für Floater mit in-arrears Zinsanpassung vorgestellt. Die Grundlagen
für die Anwendung des Forward Measure finden sich in Musiela und Rutkowski [
]
ein Modell für Floater mit in-arrears Zinsanpassung vorgestellt. Die Grundlagen
für die Anwendung des Forward Measure finden sich in Musiela und Rutkowski [![[*]](cross_ref_motif.gif) ]
und Miltersen, Sandmann und Sondermann [
]
und Miltersen, Sandmann und Sondermann [![[*]](cross_ref_motif.gif) ],
sowie sehr ausführlich in Jamshidian [
],
sowie sehr ausführlich in Jamshidian [![[*]](cross_ref_motif.gif) ].
].
Zur Bewertung von Kapitalmarktfloatern mit Bindung an einen Zinssatz mit konstanter
Laufzeit (Constant Maturity Produkten) findet sich in Jamshidian [![[*]](cross_ref_motif.gif) ]
eine ausführliche Darstellung, welche auf das Modell aus Brotherton-Ratcliffe
und Iben [
]
eine ausführliche Darstellung, welche auf das Modell aus Brotherton-Ratcliffe
und Iben [![[*]](cross_ref_motif.gif) ] zurückzuführen ist. Eine
leichter zugängliche Beschreibung des Ansatzes findet sich in Hull [
] zurückzuführen ist. Eine
leichter zugängliche Beschreibung des Ansatzes findet sich in Hull [![[*]](cross_ref_motif.gif) ].
].
Eine der ersten umfassenden Darstellungen des Bewertungsproblems für Kapitalmarktfloater
mit Bindung an einen Zinssatz mit variabler Laufzeit wurde in Pichler [![[*]](cross_ref_motif.gif) ]
vorgestellt. Im wesentlichen der gleiche Ansatz wurde auch in einem Arbeitspapier
von Frühwirth [
]
vorgestellt. Im wesentlichen der gleiche Ansatz wurde auch in einem Arbeitspapier
von Frühwirth [![[*]](cross_ref_motif.gif) ] verwendet.
] verwendet.
Bewertungsmodell
Dieser Abschnitt gibt eine Überblick über das in dieser Arbeit verwendete Bewertungsmodell
(vgl. [![[*]](cross_ref_motif.gif) ]). Der exakte Rechenvorgang wird anhand eines
konkreten Beispieles in Abschnitt
]). Der exakte Rechenvorgang wird anhand eines
konkreten Beispieles in Abschnitt ![[*]](cross_ref_motif.gif) beschrieben.
beschrieben.
Der verwendete Bewertungsansatz basiert auf einer endogenen Modellierung der SMR und einem zusätzlichen exogenen Fehlerterm, d.h. die SMR wird in zwei Teile aufgeteilt:
- Einen prognostizierbaren SMR-Teil, basierend auf den zum Bewertungszeitpunkt verfügbaren Informationen.
- Einen Fehlerprozess, der mit den dem Zinsstrukturmodell zugrundeliegenden Faktoren unkorreliert ist und die Abweichungen von der modellmäßigen SMR angibt.
| (4) |
| Tatsächliche SMR zum Zeitpunkt |
|
|
|
Prognostizierbare SMR unter der verfügbaren Informationsmenge |
| Realisation des Fehlerprozesses zum Zeitpunkt |
Da sich gezeigt hat, dass eine hohe Korrelation zwischen der SMR und einigen CMTs vorliegt, wird die SMR als Linearkombination aus mehreren CMTs dargestellt. Der lineare Zusammenhang kann durch folgende OLS Regression bestimmt werden:
| CMT mit Laufzeit |
||
|
|
Lineare Gewichtung der CMT mit Laufzeit |
|
|
|
Residualterm mit
|
Unter der Annahme, dass der Fehlerprozess und die Diskontierungsfaktoren unkorreliert sind, kann der CMT-abhängige Teil getrennt vom SMR-spezifischen Teil bewertet werden. Für den CMT-abhängigen Teil einer SMR-gebundenen Kuponzahlung gilt
wobei
![[*]](cross_ref_motif.gif) ]):
]):
| Forward-Swap-Rate
|
||
|
|
Volatilität der Forward-Swap-Rate | |
| Kuponperiode | ||
|
|
Annuitätenfaktor: Der zu |
Zur Modellierung des Fehlerprozesses wurde ein Ornstein-Uhlenbeck-Prozess mit folgendem Aussehen verwendet:
| Mean Reversion Parameter | ||
| Volatilitätsparameter | ||
| Langfristiger Mittlerwert |
Für den diskreten Fall greift man auf die Euler-Approximation des Ornstein-Uhlenbeck-Prozesses,
den sog. AR(1)-Prozess (vgl. [![[*]](cross_ref_motif.gif) ]), zurück.
Es gilt:
]), zurück.
Es gilt:
| (9) |
Für die Residualvarianz gilt weiters:
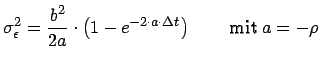 |
(10) |
Dabei bezeichnet
Der Parameter
Den Mean Reversion Paramater ![]() erhält man ebenso wie die Realisation
von
erhält man ebenso wie die Realisation
von ![]() aus der Regression. Lediglich der Parameter
aus der Regression. Lediglich der Parameter
![]() muss durch Kalibrierung an Marktdaten ermittelt werden (vgl. Abschnitt
muss durch Kalibrierung an Marktdaten ermittelt werden (vgl. Abschnitt ![[*]](cross_ref_motif.gif) ).
).
Kombiniert man die beiden Bewertungen ergibt sich als Barwert für eine zum Zeitpunkt
![]() fällige Kuponzahlung:
fällige Kuponzahlung:
![$\displaystyle \underbrace{\sum _{k=1}^{K}\left[ \beta _{k}\cdot V_{k}\left( t,T...
...t\right) }\right] }_{\textrm{Barwert des Erwartungswertes des Fehlerprozesses}}$](img71.gif) |
(14) |
Programmbedienung
Das Programm wurde in zwei Bereiche unterteilt:
- Einen Assistenten, der dialoggesteuert durch den Kalibrierungs- und Bewertungsprozess führt (Datei smr.xls).
- Eine Arbeitsmappe, welche bespielhaft die Makros zur Kalibrierung und Bewertung verwendet (Datei smrmakro.xls).
Assistent
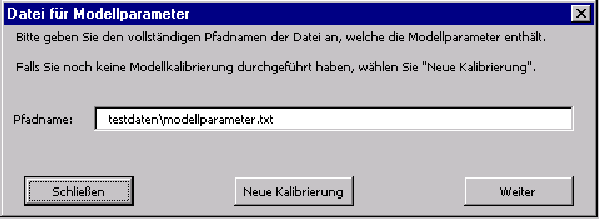
Nach dem Öffnen der Arbeitsmappe smr.xls erscheint sofort der Einstiegsdialog
des Assistenten (vgl. Abbildung ![[*]](cross_ref_motif.gif) ). Falls man eine
neue Kalibrierung durchführen will, wählt man ,,Neue Kalibrierung``. Will man
eine Bewertung basierend auf einer bestehenden Kalibrierung durchführen, muss
man den Pfadnamen der Datei mit den Kalibrierungswerten angeben und wählt dann
,,Weiter``.
). Falls man eine
neue Kalibrierung durchführen will, wählt man ,,Neue Kalibrierung``. Will man
eine Bewertung basierend auf einer bestehenden Kalibrierung durchführen, muss
man den Pfadnamen der Datei mit den Kalibrierungswerten angeben und wählt dann
,,Weiter``.
Der nachfolgende Dialog ist abhängig davon, ob man sich für eine neue Kalibrierung oder eine Bewertung entschieden hat.
Kalibrierung
Nachdem man sich im Einstiegsdialog für eine neue Kalibrierung entschieden hat
wird man in den folgenden Dialogen aufgefordert, die Dateinamen für die Zeitreihen
der Zinssätze sowie der Sekundärmarktrendite anzugeben, woraufhin diese eingelesen
werden (Für die unterstützten Dateiformate vgl. Abschnitt ![[*]](cross_ref_motif.gif) ).
Nach dem Einlesen der Zeitreihe der Sekundärmarktrendite wird überprüft, ob
sich der Datumsbereich der beiden Zeitreihen ausreichend überschneidet. Nur
in diesem Fall kann mit der Kalibrierung fortgefahren werden und man gelangt
zum Hauptdialog der Kalibrierung (vgl. Abbildung
).
Nach dem Einlesen der Zeitreihe der Sekundärmarktrendite wird überprüft, ob
sich der Datumsbereich der beiden Zeitreihen ausreichend überschneidet. Nur
in diesem Fall kann mit der Kalibrierung fortgefahren werden und man gelangt
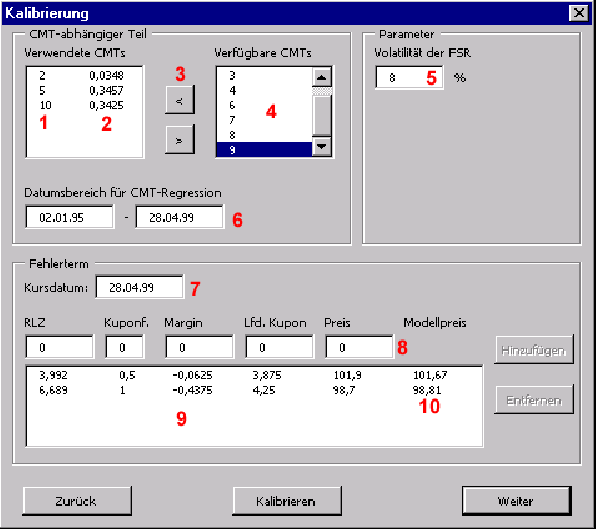
zum Hauptdialog der Kalibrierung (vgl. Abbildung ![[*]](cross_ref_motif.gif) ).
).
|
Der Hauptdialog gliedert sich in drei Teile:
- Auswahl der zu verwendenden CMTs sowie des Zeitbereichs für die Regression.
- Angabe der Volatilität der Forward Swap Rate zur Bewertung der CMT-angepassten Zahlungen.
- Stammdaten und Kurse jener Anleihen, die zur Kalibrierung des Fehlerterms (konkret:
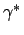 ) verwendet werden sollen.
) verwendet werden sollen.
![[*]](cross_ref_motif.gif) erklärt. Erwähnenswert ist, dass in der Anleihenliste (9) einzelne Werte markiert
werden können. Diese werden bei der darauffolgenden Kalibrierung nicht
berücksichtigt.
erklärt. Erwähnenswert ist, dass in der Anleihenliste (9) einzelne Werte markiert
werden können. Diese werden bei der darauffolgenden Kalibrierung nicht
berücksichtigt.
Nachdem eine Kalibrierung durchgeführt wurde (Schaltfläche ,,Kalibrieren``), werden in der Anleihenliste zusätzlich die ermittelten Modellpreise angezeigt. Sollte es hier zu größeren Abweichungen kommen, ist es ratsam die eingegebenen Werte nochmals zu überprüfen bzw. die Auswahl der Anleihen zu überdenken.
Sobald die Kalibrierung abgeschlossen ist gelangt man mittels ,,Weiter`` in den letzten Dialog, innerhalb dessen man angeben kann, in welcher Datei die ermittelten Werte für eine spätere Bewertung gespeichert werden sollen. Außerdem können in diesem Dialog die Kalibrierungswerte mittels ,,Drucken`` ausgedruckt werden.
Bewertung
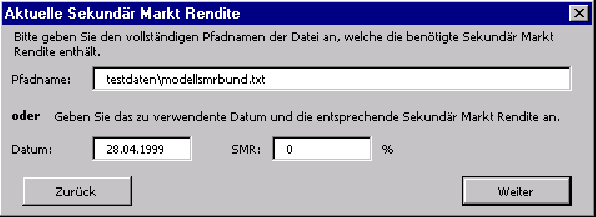
Nach dem man im Einstiegsdialog die Datei mit den Kalibrierungswerten und im
nächsten Dialog die Datei für die aktuellen Zinssätze angegeben hat, gelangt
man in den Dialog für die aktuelle Sekundärmarktrendite (vgl. Abbildung ![[*]](cross_ref_motif.gif) ).
Da zur Bewertung nur die aktuelle SMR benötigt wird, kann hier neben einer Datei,
welche mehrere SMR-Daten enthalten kann, auch eine SMR mit dem zugehörigen Datum
direkt angeben werden.
).
Da zur Bewertung nur die aktuelle SMR benötigt wird, kann hier neben einer Datei,
welche mehrere SMR-Daten enthalten kann, auch eine SMR mit dem zugehörigen Datum
direkt angeben werden.
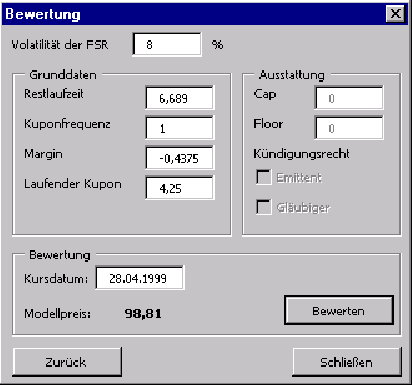
![[*]](cross_ref_motif.gif) ). Neben der Volatilität der Forward Swap Rate
müssen im Bereich ,,Grunddaten`` die Daten der zu bewertenden Anleihe sowie
im Bereich ,,Bewertung`` das Kursdatum eingegeben werden. Danach kann diese
Anleihe bewertet werden (Schaltfläche ,,Bewerten``), woraufhin der Modellpreis
unterhalb des Kursdatums angezeigt wird.
). Neben der Volatilität der Forward Swap Rate
müssen im Bereich ,,Grunddaten`` die Daten der zu bewertenden Anleihe sowie
im Bereich ,,Bewertung`` das Kursdatum eingegeben werden. Danach kann diese
Anleihe bewertet werden (Schaltfläche ,,Bewerten``), woraufhin der Modellpreis
unterhalb des Kursdatums angezeigt wird.
Der Bereich ,,Ausstattung`` wurde nicht implementiert, da eine Bewertung von Optionsrechten den Rahmen dieser Arbeit sprengen würde.
Makros
Das Excel-Addin smr.xla stellt unter anderem auch Makrofunktionen zur
Verfügung, die es erlauben ohne den Assistenten innerhalb einer Arbeitsmappe
mehrere Kalibrierungen und Bewertungen gleichzeitig durchzuführen. Die Arbeitsmappe
smrmakro.xls enthält einige Beispiele zur Anwendung dieser Makros.
Eine genaue Beschreibung der Parameter ist in Abschnitt ![[*]](cross_ref_motif.gif) zu
finden.
zu
finden.
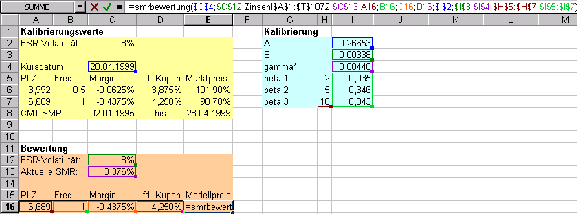
In den Abbildungen ![[*]](cross_ref_motif.gif) und
und ![[*]](cross_ref_motif.gif) sind Beispiele zur Kalibrierung und Bewertung dargestellt.
sind Beispiele zur Kalibrierung und Bewertung dargestellt.

|
|
Programmbeschreibung
Dieser Abschnitt gibt einen Überblick über die Funktionsweise des Programmes.
Dazu werden in ![[*]](cross_ref_motif.gif) und
und ![[*]](cross_ref_motif.gif) die Klassen und Makros
beschrieben, die im AddIn smr.xla enthalten sind. In
die Klassen und Makros
beschrieben, die im AddIn smr.xla enthalten sind. In ![[*]](cross_ref_motif.gif) wird abschließend anhand eines konkreten Beispiels der Ablauf des Kalibrierungs-
und Bewertungsvorganges erläutert.
wird abschließend anhand eines konkreten Beispiels der Ablauf des Kalibrierungs-
und Bewertungsvorganges erläutert.
Klassen
Klasse ,,Spotrates``
Diese Klasse repräsentiert eine Zinsstruktur für verschiedene Datumswerte. Die
Werte der Zinsstruktur können aus einer Datei (vgl. Abschnitt ![[*]](cross_ref_motif.gif) )
bzw. direkt aus einem Tabellenblatt eingelesen und danach beliebig abgefragt
werden. Zwischen den vorhandenen Laufzeiten werden die Zinssätze linear interpoliert.
)
bzw. direkt aus einem Tabellenblatt eingelesen und danach beliebig abgefragt
werden. Zwischen den vorhandenen Laufzeiten werden die Zinssätze linear interpoliert.
| Methode | Funktion |
| getAF | Berechnet den Annuitätenfaktor basierend auf der aktuellen Zinsstruktur. |
| getAvailableDates | Liefert ein einspaltiges Datenfeld, welches alle verfügbaren Datumswerte in absteigender Reihenfolge enthält. |
| getAvailableMaturities | Liefert ein einspaltiges Datenfeld, welches alle verfügbaren Laufzeiten in aufsteigender Reihenfolge enthält. |
| getDiscountFactor | Berechnet den Diskontierungsfaktor basierend auf der aktuellen Zinsstruktur. |
| getFirstDate | Ermittelt das älteste Datum für welches eine Zinsstruktur vorliegt. |
| getForwardRate | Berechnet die Forward Rate basierend auf der aktuellen Zinsstruktur. |
| getForwardSwapRate | Berechnet die Forward Swap Rate basierend auf der aktuellen Zinsstruktur. |
| getHistoryAF | Berechnet den Annuitätenfaktor basierend auf der Zinsstruktur zum angegebenen Datum. |
| getHistoryDiscountFactor | Berechnet den Diskontierungsfaktor basierend auf der Zinsstruktur zum angegebenen Datum. |
| getHistoryForwardRate | Berechnet die Forward Rate basierend auf der Zinsstruktur zum angegebenen Datum. |
| getHistoryForwardSwapRate | Berechnet die Forward Swap Rate basierend auf der Zinsstruktur zum angegebenen Datum. |
| getHistoryRateFor | Liefert den Zinssatz für die angegebene Laufzeit zum angegebenen Datum. Liegt diese Information nicht vor, wird der Wert 0 zurückgegeben. |
| getHistorySwapRate | Berechnet die Swap Rate basierend auf der Zinsstruktur zum angegebenen Datum. |
| getLastDate | Ermittelt das jüngste Datum für welches eine Zinsstruktur vorliegt. |
| getRateFor | Liefert den Zinssatz für die angegebene Laufzeit für das aktuelle Datum. |
| getSwapRate | Berechnet die Swap Rate basierend auf der aktuellen Zinsstruktur. |
| isOK | Liefert true, falls das Objekt korrekt initialisiert worden ist und eine Zinsstruktur eingelesen wurde. |
| read | Liest die Zinsstruktur aus einer Datei ein. Konnte die angegebene Datei gefunden werden, wird readStandard aufgerufen, anderenfalls readPL. |
| readFromMatrix | Liest die Zinsstruktur aus einem Tabellenblatt ein. Falls der markierte Bereich zweispaltig ist, müssen in der ersten Spalte die Laufzeiten und in der zweiten Spalte die aktuellen Zinssätze stehen. Enthält der Bereich mehr als zwei Spalten, müssen in der ersten Zeile die Laufzeiten stehen, in der ersten Spalte die Datumswerte und in den restlichen Feldern die entsprechenden Zinssätze. |
| readPL | Liest die Zinsstruktur aus mehreren Dateien im ProfitLine-Format ein. Die Namen der Dateien müssen dem Format XXXYY.ZZZ entsprechen, wobei XXX und ZZZ beliebige Buchstaben sein dürfen und YY der Laufzeit entspricht. |
| readStandard | Liest die Zinsstruktur aus einer Datei im Standard-Format ein. Die Datei muss einer Zinsmatrix entsprechend aufgebaut sein (vgl. readFromMatrix), wobei die Spalten durch einen Tabulator (chr(9)) getrennt sein müssen. |
| setRates | Liest die aktuelle Zinsstruktur aus einem Tabellenblatt ein. Der markierte Bereich muss zweispaltig sein, wobei in der ersten Spalte die Laufzeiten und in der zweiten Spalte die aktuellen Zinssätze stehen müssen. |
Verwendete Berechnungsmethoden
- Annuitätenfaktor
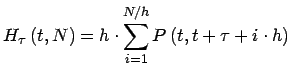
(15)
Der zu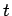 beobachtbare Preis einer zu
beobachtbare Preis einer zu 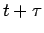 beginnenden Annuität
über
beginnenden Annuität
über 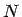 Jahre mit Kuponfrequenz
Jahre mit Kuponfrequenz 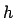 .
. - Forward Rate
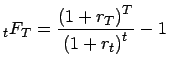
(16)
- Forward Swap Rate
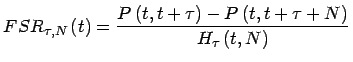
(17)
- Swap Rate
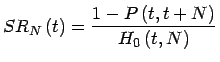
(18)
Klasse ,,CMT``
Diese Klasse liefert basierend auf einer Zinsstruktur (Objekt der Spotrates-Klasse) die Constant Maturity Treasury-Werte.
| Methode | Funktion |
| getAvailableDates | Liefert ein einspaltiges Datenfeld, welches alle verfügbaren Datumswerte in absteigender Reihenfolge enthält. |
| getAvailableMaturities | Liefert ein einspaltiges Datenfeld, welches alle verfügbaren Laufzeiten in aufsteigender Reihenfolge enthält. |
| getConvexityAdjustment | Berechnet das sog. Convexity Adjustment basierend auf der aktuellen Zinsstruktur. |
| getFirstDate | Ermittelt das älteste Datum für welches eine Zinsstruktur vorliegt. |
| getHistoryConvexityAdjustment | Berechnet das sog. Convexity Adjustment basierend auf der Zinsstruktur für das angegebene Datum. |
| getHistoryRateFor | Liefert den CMT-Wert für die angegebene Laufzeit zum angegebenen Datum. Liegt diese Information nicht vor, wird der Wert 0 zurückgegeben. |
| getLastDate | Ermittelt das jüngste Datum für welches eine Zinsstruktur vorliegt. |
| getPaymentValue | Berechnet den Barwert einer Kuponzahlung mit perfekter regulärer Zinsanpassung an eine CMT. |
| getRateFor | Liefert den aktuellen CMT-Wert für die angegebene Laufzeit. Liegt diese Information nicht vor, wird der Wert 0 zurückgegeben. |
| getValue | Berechnet den Barwert einer Anleihe mit perfekter regulärer Zinsanpassung an eine CMT. |
| setSpotRates | Weist das zu verwendende SpotRates-Objekt zu. Alle Berechnungen basieren auf der Zinsstruktur diese Objektes. |
Verwendete Berechnungsmethoden
- CMT-Wert
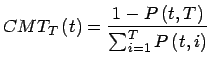
(19)
- Convexity Adjustment
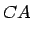
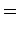
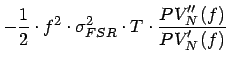
(20) 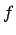
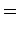
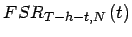
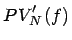
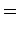
![$\displaystyle -f\cdot \sum _{i=1}^{N}\left[ i\cdot \left( 1+f\right) ^{-i-1}\right] -N\cdot \left( 1+f\right) ^{-N-1}$](img90.gif)
(21) 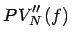
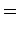
![$\displaystyle f\cdot \sum _{i=1}^{N}\left[ i\cdot \left( i+1\right) \cdot \left...
...right) ^{-i-2}\right] +N\cdot \left( N+1\right) \cdot \left( 1+f\right) ^{-N-2}$](img43.gif)
(22)
- Barwert einer Kuponzahlung mit perfekter regulärer Zinsanpassung an eine CMT
Klasse ,,SMR``
Diese Klasse abstrahiert SMR-Werte für verschiedene Datumswerte. Die SMR-Werte
können aus einer Datei (vgl. Abschnitt ![[*]](cross_ref_motif.gif) ) bzw. direkt
aus einem Tabellenblatt eingelesen und danach beliebig abgefragt werden.
) bzw. direkt
aus einem Tabellenblatt eingelesen und danach beliebig abgefragt werden.
| Methode | Funktion |
| getAvailableDates | Liefert ein einspaltiges Datenfeld, welches alle verfügbaren Datumswerte in absteigender Reihenfolge enthält. |
| getFirstDate | Ermittelt das älteste Datum für welches SMR-Werte vorliegen. |
| getHistoryRate | Liefert den SMR-Wert für das angegebene Datum. Liegt diese Information nicht vor, wird der Wert 0 zurückgegeben. |
| getLastDate | Ermittelt das jüngste Datum für welches SMR-Werte vorliegen. |
| getRate | Liefert den SMR-Wert für das aktuelle Datum. Liegt diese Information nicht vor, wird der Wert 0 zurückgegeben. |
| isOK | Liefert true, falls das Objekt korrekt initialisiert worden ist und SMR-Werte eingelesen wurden. |
| read | Liest die Zinsstruktur aus einer Datei ein. Konnte die angegebene Datei gefunden werden, wird readStandard aufgerufen, anderenfalls readPL. |
| readFromMatrix | Liest die SMR-Werte aus einem Tabellenblatt ein. Der markierte Bereich muss zweispaltig sein und in der ersten Spalte die Datumswerte und in der zweiten Spalte die entsprechenden SMR-Werte enthalten. |
| readPL | Liest die SMR-Werte aus einer Datei im ProfitLine-Format ein. |
| readStandard | Liest die SMR-Werte aus einer Datei im Standard-Format ein. Die Datei muss genau so aufgebaut sein wie eine SMR-Matrix (vgl. readFromMatrix), wobei die Spalten durch einen Tabulator (chr(9)) getrennt sein müssen. |
| setRate | Setzt den SMR-Werte für das aktuelle Datum. |
Klasse ,,SMRRegression``
In dieser Klasse ist der Algorithmus zur Bewertung SMR-abhängiger Kuponzahlungen implementiert.
| Methode | Funktion |
| addCalibrateValue | Fügt die Stammdaten einer Anleihe zur internen Liste hinzu, welche für die Fehlerterm-Kalibrierung verwendet wird. |
| berechneParameter | Berechnet die Modellparameter |
| berechneUT | Berechnet das aktuelle |
| calibrate | Bereitet die Daten zur Kalibrierung vor (createArrays) und ruft danach die Methoden schätzeRoh, schätzeBetas und berechneParameter auf. |
| checkSecondDimension | Hilfsfunktion um sicherzustellen, dass ein Array zweidimensional ist. |
| createArrays | Erstellt die Arrays für die CMT- und SMR-Werte sowie die
|
| eDach | Hilfsfunktion für schätzeRoh. |
| getA | Liefert den Modellparameter |
| getActualDate | Liefert das ,,aktuelle`` Datum. |
| getB | Liefert den Modellparameter |
| getBetas | Liefert ein einspaltiges Array mit den |
| getCalibrationCMTMaturities | Liefert die Laufzeiten der CMTs, welche für den CMT-abhängigen Teil verwendet werden. |
| getCalibrationEndDate | Liefert das Enddatum, bis zu welchem die SMR-Regression durchgeführt werden soll. |
| getCalibrationStartDate | Liefert das Anfangsdatum, ab welchem die SMR-Regression durchgeführt werden soll. |
| getCalibrationValues | Liefert ein fünfspaltiges Array, welches die Stammdaten jener Anleihen enthält, die zur Kalibrierung des Fehlerterms verwendet werden sollen. |
| getDetailValue | Liefert ein vierspaltiges Array. Ausgehend von den übergebenen Stammdaten wird eine Bewertung vorgenommen. Das Array enthält (in genau dieser Reihenfolge) folgende Barwerte: CMT-Teil, SMR-Teil, Stückzinsen, Margin. |
| getFSRVolatility | Liefert die Volatilität der Forward Swap Rate. |
| getGamma | Liefert das ermittelte |
| getGammaStern | Liefert das ermittelte
|
| getLambda | Liefert das ermittelte |
| getPresentValue | Bewertung des SMR-abhängigen Fehlerterms. |
| getValue | Führt eine Bewertung für die übergebenen Stammdaten durch. Entspricht der Summe von getDetailValue. |
| initValuation | Initialisiert das Objekt für eine Bewertung. Es werden die notwendigen Arrays
aufgebaut (createArrays) und das aktuelle |
| isCalibrated | Liefert true, falls das Objekt gültige Modellparameter enthält. |
| readFromFile | Liest die Modellparameter aus einer Datei, welche mit writeToFile erstellt wurde. |
| resetCalibration | Setzt die Kalibrierung zurück. |
| schätzeBetas | Schätzt aus den
|
| schätzeRoh | Ermittelt den Wert |
| setActualDate | Setzt das ,,aktuelle`` Datum. |
| setCMT | Übergibt das zu verwendende CMT-Objekt. |
| setFSRVolatility | Setzt die Volatilität der Forward Swap Rate. |
| setParameter | Setzt die Modellparameter |
| setSMR | Übergibt das zu verwendende SMR-Objekt. |
| setSpotRates | Übergibt das zu verwendende SpotRates-Objekt. |
| writeToFile | Schreibt die Modellparameter in eine Datei. |
Auf die Berechnungsmethoden wird detailiert im konkreten Beispiel (Abschnitt
![[*]](cross_ref_motif.gif) ) eingegangen.
) eingegangen.
Makros
SMRKalibrierung
- Definition:
- Public Function SMRKalibrierung(
vspots as Variant,
vsmr as Variant,
vkali as Variant,
vcmt as Variant,
fsrvol as Variant,
smrvon as Variant,
smrbis as Variant,
kursdatum as Date) As Variant
| Parameter | Beschreibung |
| vspots | Entweder der Name der Datei mit den Zeitreihen der Zinssätze oder ein einzelner Zellenbereich, der die Zeitreihen enthält. |
| vsmr | Entweder der Name der Datei mit der Zeitreihe der SMR oder ein einzelner Zellenbereich, der die Zeitreihe enthält. |
| vkali | Ein Zellenbereich, der die Stammdaten jener Anleihen enthält, welche zur Kalibrierung verwendet werden sollen. Der Zellenbereich muss exakt fünf Spalten breit sein, in denen die Werte Restlaufzeit, Kuponfrequenz, Margin, laufender Kupon und Marktpreis in genau dieser Reihenfolge enthalten sind. Jede Zeile beschreibt eine einzelne Anleihe. |
| vcmt | Ein Zellenbereich mit exakt einer Spalte, welcher die zu verwendenden CMTs angibt. |
| fsrvol | Volatilität der Forward Swap Rate. |
| smrvon | Anfangsdatum, ab dem die SMR-Regression durchgeführt wird. |
| smrbis | Enddatum, bis zu dem die SMR-Regression durchgeführt wird. |
| kursdatum | Kursdatum der Anleihen (siehe vkali) |
- Rückgabe:
- Man erhält eine einspaltige Matrix, welche die Parameter
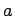 ,
,
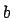 , und
, und
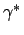 in den ersten drei Zeilen enthält und in den
folgenden Zeilen die
in den ersten drei Zeilen enthält und in den
folgenden Zeilen die 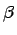 -Werte.
-Werte.
SMRBewertung
- Definition:
- Public Function SMRBewertung(
kursdatum As Date,
vol As Double,
vspots As Variant,
vsmr As Variant,
rlz As Double,
freq As Double,
margin As Double,
kupon As Double,
par As Variant,
Optional parB As Double = 0,
Optional parGammaStern As Double = 0,
Optional parCMTs As Variant,
Optional parBetas As Variant) As Double
| Parameter | Beschreibung |
| kursdatum | Datum für die Bewertung. Notwendig, falls Zinssätze bzw. SMR-Werte für mehrere Datumswerte angegeben wurden. |
| vol | Volatilität der Forward Swap Rate. |
| vspots | Entweder der Name der Datei, welche die Zinssätze enthält oder ein Zellbereich, welcher in der ersten Zeile die Laufzeiten enthält, in der ersten Spalte die Datumswerte und in den restlichen Feldern die entsprechenden Zinssätze. |
| vsmr | Entweder der Name der Datei, welche die SMR-Zeitreihe enthält oder ein Zellbereich, welcher in der ersten Spalte die Datumswerte und in der zweiten Spalte die entsprechenden SMR-Werte enthält. |
| rlz | Restlaufzeit der zu bewertenden Anleihe |
| freq | Kuponfrequenz |
| margin | Margin |
| kupon | Laufender Kupon |
| par | Entweder der Name der Datei, welche die Modellparameter enthält oder der Modellparameter
|
| parB | Modellparameter |
| parGammaStern | Modellparameter
|
| parCMTs | Ein Zellenbereich mit exakt einer Spalte, welcher die Laufzeiten der verwendeten CMTs enthält. |
| parBetas | Ein Zellenbereich mit exakt einer Spalte, welcher die |
- Rückgabe:
- Modellpreis der Anleihe
SMRDetailBewertung
- Definition:
- Public Function SMRDetailBewertung(
kursdatum As Date,
vol As Double,
vspots As Variant,
vsmr As Variant,
rlz As Double,
freq As Double,
margin As Double,
kupon As Double,
par As Variant,
Optional parV As Double = 0,
Optional parGammaStern As Double = 0,
Optional parCMTs As Variant,
Optional parBetas As Variant) As Variant
- Rückgabe:
- Ein einzeilige Matrix welche die Barwerte des CMT-Teils, des SMR-Teils, der Stückzinsen und der Margin in genau dieser Reihenfolge enthält. Die Summe dieser vier Werte entspricht dem Rückgabewert der Funktion SMRBewertung.
Beispiel
In diesem Abschnitt wird anhand eines konkreten Beispiels der Kalibrierungs- und Bewertungsvorgang dargestellt. Es werden jeweils die relevanten Formeln sowie die Rechenergebnisse angeführt. Die Methoden, welche die Berechnungen durchführen, werden im Format {Klasse:Methode} bzw. {Prozedur} angeführt (z.B. {SMR:createArrays}), wobei der Programmablauf bei Einsatz der Makros beschrieben wird.
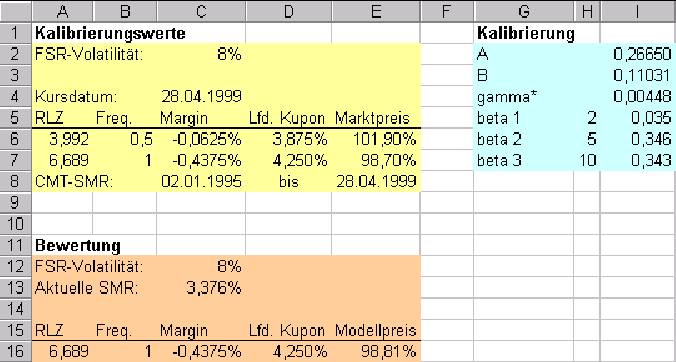
Dieses Beispiel ist in der Arbeitsmappe smrmakro.xls auf der Seite
,,Beispiel`` zu finden (vgl. Abbildung ![[*]](cross_ref_motif.gif) ).
).
Kalibrierung
In diesem Abschnitt wird die Kalibrierung des Bewertungsmodells beschrieben.
Es werden mittels einer AR(1)-Regression die linearen Gewichtungen der CMTs
(vgl. Formel ![[*]](cross_ref_motif.gif) ) sowie der Mean Reversion Parameter
) sowie der Mean Reversion Parameter
![]() (vgl. Formel
(vgl. Formel ![[*]](cross_ref_motif.gif) ) ermittelt. Der risikoadjustierte
langfristige Mittelwert
) ermittelt. Der risikoadjustierte
langfristige Mittelwert
![]() des Fehlerprozesses wird anschließend
mittels eines einfachen iterativen Verfahrens an den Daten ausgewählter Anleihen
kalibriert.
des Fehlerprozesses wird anschließend
mittels eines einfachen iterativen Verfahrens an den Daten ausgewählter Anleihen
kalibriert.
Die Regression wird im Zeitraum 2.1.1995 bis 28.4.1999 durchgeführt. Zur Kalibrierung
des Fehlerterms werden die Anleihen 13772 und 42804 (vgl. Tabelle ![[*]](cross_ref_motif.gif) )
zusammen mit ihren Marktdaten vom 28.4.1999 verwendet (vgl. Tabelle
)
zusammen mit ihren Marktdaten vom 28.4.1999 verwendet (vgl. Tabelle ![[*]](cross_ref_motif.gif) ).
).
|
|
In einem ersten Schritt werden die Objekte für die Zinssätze, SMR- und CMT-Werte erzeugt {SMRKalibrierung} und mit den entsprechenden Daten gefüllt. Diese werden dann zusammen mit den notwendigen Stamm- und Marktdaten der Anleihen dem SMRRegression-Objekt übergeben und danach die Kalibrierung durch Aufruf der Methode {SMRRegression:calibrate} angestoßen. Es werden nun die folgenden Vorgänge ausgeführt:
- Erstellung der notwendigen Datenfelder (
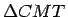 ,
,
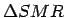 )
für die Regression (Seite
)
für die Regression (Seite ![[*]](cross_ref_motif.gif) ).
). - Schätzung des
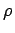 -Wertes für die AR1-Regression (Seite
-Wertes für die AR1-Regression (Seite ![[*]](cross_ref_motif.gif) ).
). - Schätzung der
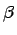 -Werte (Seite
-Werte (Seite ![[*]](cross_ref_motif.gif) ).
). - Berechnung der Modellparameter (Seite
![[*]](cross_ref_motif.gif) ).
).
Erstellung der Datenfelder
Da im verwendeten Modell die Änderungen der SMR durch Änderungen einer Linearkombination
der CMT-Werte beschrieben werden (vgl. Formel ![[*]](cross_ref_motif.gif) ),
ist es notwendig die
),
ist es notwendig die
![]() - und
- und
![]() -Werte zu berechnen
und für eine weitere Verwendung temporär ab zu speichern {SMRRegression:createArrays}.
-Werte zu berechnen
und für eine weitere Verwendung temporär ab zu speichern {SMRRegression:createArrays}.
Schätzung von
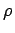
Da für die (diskrete) Modellierung des Fehlerterms ein AR(1)-Prozess verwendet
wird, muss zuerst der Parameter ![]() berechnet werden {SMRRegression:schätzeRoh}
(vgl. [
berechnet werden {SMRRegression:schätzeRoh}
(vgl. [![[*]](cross_ref_motif.gif) ]), bevor die
]), bevor die ![]() -Werte
geschätzt werden können. Man beginnt indem man erste Schätzwerte für
die
-Werte
geschätzt werden können. Man beginnt indem man erste Schätzwerte für
die ![]() -Werte berechnet:
-Werte berechnet:
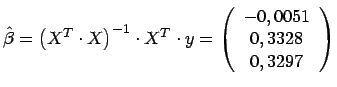 |
(24) |
Dabei bezeichnen
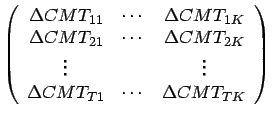 |
|||
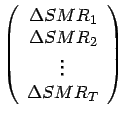 |
Ausgehend von diesen Werten kann man nun zuerst einen Schätzwert für
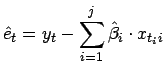 |
(25) |
und anschließend
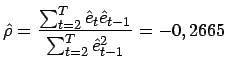 |
(26) |
Schätzung der
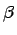 -Werte
-Werte
Nachdem
![]() berechnet wurde, können nun die
berechnet wurde, können nun die ![]() -Werte
auf folgende Art geschätzt werden {SMRRegression:schätzeBetas}:
-Werte
auf folgende Art geschätzt werden {SMRRegression:schätzeBetas}:
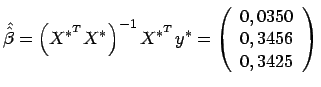 |
(27) |
Dabei gilt:
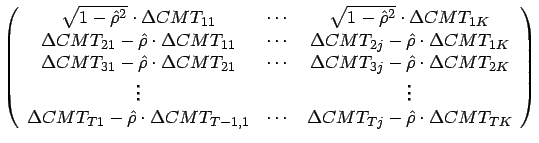 |
|||
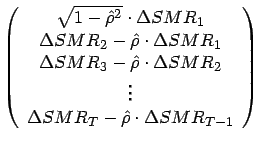 |
Weiters berechnet man einen Schätzwert für die Residualvarianz![[*]](foot_motif.gif) :
:
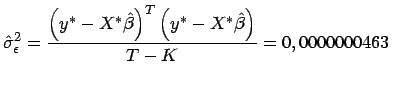 |
(28) |
Auf Basis der geschätzten ![]() -Werte kann man den momentanen Wert des
Fehlerterms mittels Formel
-Werte kann man den momentanen Wert des
Fehlerterms mittels Formel ![[*]](cross_ref_motif.gif) berechnen zu
berechnen zu
![]() {SMRRegression:berechneUT}.
{SMRRegression:berechneUT}.
Berechnung der Modellparameter
Abschließend müssen noch die Modellparameter basierend auf den Ergebissen der
Regression berechnet werden {SMRRegression:berechneParameter}:
| (29) | |||
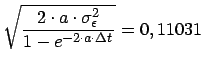 |
(30) | ||
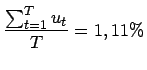 |
(31) | ||
Der Wert
![[*]](cross_ref_motif.gif) ab Zeile 600).
ab Zeile 600).
Bewertung
Basierend auf der Kalibrierung aus vorherigem Abschnitt wird nun die Anleihe
42804 bewertet {SMRBewertung}. Dazu wird für jede einzelne Kuponzahlungen
eine Bewertung durchgeführt {SMRRegression:getDetailValue} (vgl.
Tabelle ![[*]](cross_ref_motif.gif) ). Zu beachten ist dabei, dass für
die erste Zahlungen nur der laufende Kupon heranzuziehen ist, aber weder Fehlerterm
noch Margin zu berücksichtigen sind. Es gilt die aus Abschnitt
). Zu beachten ist dabei, dass für
die erste Zahlungen nur der laufende Kupon heranzuziehen ist, aber weder Fehlerterm
noch Margin zu berücksichtigen sind. Es gilt die aus Abschnitt ![[*]](cross_ref_motif.gif) bekannte Formel:
bekannte Formel:
![$\displaystyle V\left( t,T\right) =\underbrace{\sum _{k=1}^{K}\left[ \beta _{k}\...
...t\right) }\right] }_{\textrm{Barwert des Erwartungswertes des Fehlerprozesses}}$](img123.gif)
![[*]](cross_ref_motif.gif) ).
).
|
Nun müssen von der Summe der Barwerte der einzelnen Kuponzahlung noch die Stückzinsen abgezogen und der Barwert der Rückzahlung addiert werden. Somit ergibt sich folgender Wert:
| Kuponzahlungen | 21,974 |
| Rückzahlung | 71,156 |
| Stückzinsen | -1,322 |
| Gesamt | 98,808 |
Dateiformate
Die Klassen SMR, SpotRates und SMRRegression können ihre Daten aus speziell formatierten Dateien einlesen. Dieser Abschnitt beschreibt das Format dieser Dateien.
Zinssätze
Die Klasse SpotRates kann zwei verschiedene Datenformate verarbeiten:
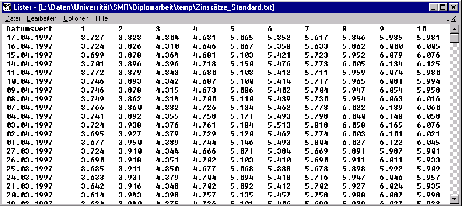
- Standardformat
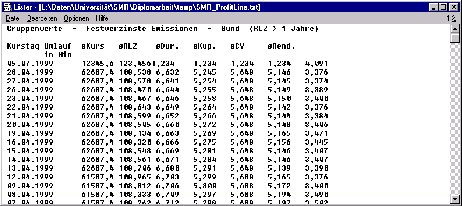
Die Datei ist eine tabellenartig aufgebaute Textdatei (vgl. Abbildung
![[*]](cross_ref_motif.gif) ),
wobei die Spalten durch Tabulator-Zeichen getrennt sind. Die erste Spalte enthält
ab der zweiten Zeile die Datumswerte in absteigender Reihenfolge. Die erste
Zeile enthält ab der zweiten Spalte die Laufzeiten. Der Wert in der ersten Zeile
und Spalte wird ignoriert. Ab der zweiten Zeile und Spalte müssen die entsprechenden
Zinssätze gespeichert sein.
),
wobei die Spalten durch Tabulator-Zeichen getrennt sind. Die erste Spalte enthält
ab der zweiten Zeile die Datumswerte in absteigender Reihenfolge. Die erste
Zeile enthält ab der zweiten Spalte die Laufzeiten. Der Wert in der ersten Zeile
und Spalte wird ignoriert. Ab der zweiten Zeile und Spalte müssen die entsprechenden
Zinssätze gespeichert sein.
- ProfitLine-Format
Die Daten können auch im Export-Format der Software ProfitLine (vgl. Abbildung
![[*]](cross_ref_motif.gif) ) vorliegen. Da hierbei jede Datei nur eine Zeitreihe
für eine Laufzeit enthalten kann, müssen mehrere Dateien exportiert werden.
Die Dateinamen der einzelnen Dateien müssen dem Muster XXXYY.ZZZ folgen,
wobei XXX beliebige Buchstaben (keine Zahlen) sein dürfen, die für
alle unterschiedlichen Laufzeiten identisch sein müssen und YY die
Laufzeit mit ,, . `` (Punkt) als Kommazeichen bezeichnet. Gültige Dateinamen
wären z.B. zins1.0.txt oder Spotrates_9.5.txt .
) vorliegen. Da hierbei jede Datei nur eine Zeitreihe
für eine Laufzeit enthalten kann, müssen mehrere Dateien exportiert werden.
Die Dateinamen der einzelnen Dateien müssen dem Muster XXXYY.ZZZ folgen,
wobei XXX beliebige Buchstaben (keine Zahlen) sein dürfen, die für
alle unterschiedlichen Laufzeiten identisch sein müssen und YY die
Laufzeit mit ,, . `` (Punkt) als Kommazeichen bezeichnet. Gültige Dateinamen
wären z.B. zins1.0.txt oder Spotrates_9.5.txt .
SMR
Ebenso wie die Klasse SpotRates kann auch die Klasse SMR zwei verschiedene Datenformate verarbeiten:
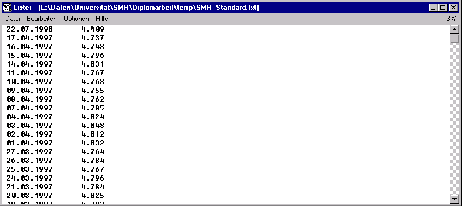
- Standardformat
In diesem Format muss die Datei zwei durch Tabulator-Zeichen getrennte Spalten enthalten. Die erste Spalte enthält dabei die Datumswerte in absteigender Reihenfolge; die zweite Spalte die entsprechenden SMR-Werte (vgl. Abbildung
![[*]](cross_ref_motif.gif) ).
).
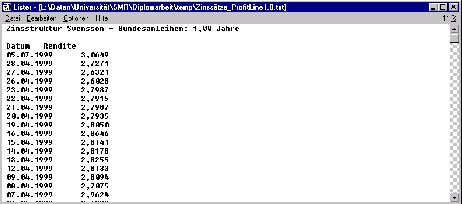
- ProfitLine-Format
Aus ProfitLine exportierte SMR-Zeitreihen (vgl. Abbildung
![[*]](cross_ref_motif.gif) )
können ohne Einschränkung eingelesen werden.
)
können ohne Einschränkung eingelesen werden.
Modellparameter
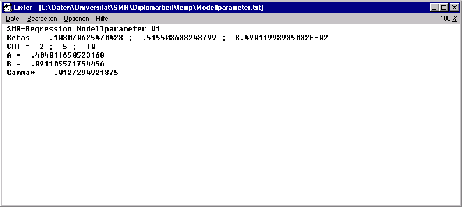
Die Klasse SMRRegression kann die ermittelten Modellparameter in eine Textdatei
(vgl. Abbildung ![[*]](cross_ref_motif.gif) ) schreiben {SMRRegression:writeToFile}
und die Parameter zur Bewertung aus der Textdatei wieder einlesen {SMRRegression:readFromFile}.
Die erste Zeile muss den Text
) schreiben {SMRRegression:writeToFile}
und die Parameter zur Bewertung aus der Textdatei wieder einlesen {SMRRegression:readFromFile}.
Die erste Zeile muss den Text
enthalten. Die weiteren Zeilen sind im Format
gehalten. Als Parameter werden erkannt:
- A
- B
- Gamma*
- Betas
- CMT
Literatur
- A
- R. Brotherton-Ratcliffe, B. Iben: Yield Curve Applications of Swap Products, in: R. Schwartz, C. Smith: Advanced Strategies in Financial Risk Management, New York Institute of Finance, New York, 1993.
- B
- Derivatives Week: CMT-Based Derivatives, Institutional Investors, 1994.
- C
- F.J. Fabozzi: Floating Rate Instruments: Characteristics, Valuation, and Portfolio Strategy, Prentice Hall, Englewood Cliffs, 1986.
- D
- M. Frühwirth: Suggestions for the Pricing of Secondary Market Yield based Floating Rate Notes subject to default Risk, Working Paper, Wirtschaftsuniversität Wien, Wien, 1998.
- E
- W. Griffiths, R. Hill, G. Judge: Learning and Practicing Econometrics, John Wiley & Sons Inc., 1993.
- F
- J.C. Hull: Options, Futures, and other Derivatives, Prentice Hall, Upper Saddle River, 1997.
- G
- F. Jamshidian: LIBOR and Swap Market Models and Measures, Finance and Stochastics 1, p. 293-330, 1997.
- H
- P. E. Kloeden, E. Platen und H. Schurz: Numerical Solutions of SDE Through Computer Experiments, Springer, New York, 1994.
- I
- A. Li und V.R. Raghavan: LIBOR In-Arrears Swaps, The Journal of Derivatives 3, p. 44-48, 1996.
- J
- K.R. Miltersen, K. Sandmann, D.Sondermann: Closed Form Solutions for Term Structure Derivatices with Log-Normal Interest Rates, The Journal of Finance 52, p. 409-430, March 1997.
- K
- M. Musiela, M. Rutkowski: Continuos-Time Term Structure Models: Forward Measure Approach, Finance and Stochastics 1, p.261-291, 1997.
- L
- Österreichische Kontrollbank: Dokumentation zur Berechnung der SMR, Wien, 1997.
- M
- S. Pichler: Bewertung von Zahlungsströmen mit variabler Verzinsung, Deutscher Universitäts Verlag, Gabler Edition Wissenschaft, 1999.
- N
- K. Ramaswamy, S. M. Sundaresan: The Valuation of Floating-Rate Instruments: Theory and Evidence, Journal of Financial Economics 17, p. 251-272, 1986.
Über dieses Dokument ...
Bewertung von SMR-ProduktenMartin Vonwald
This document was generated using the LaTeX2HTML translator Version 99.1 release (March 30, 1999)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -split 0 -local_icons -no_footnode -no_navigation -html_version 4.0 -dir ./html Bewertung_von_SMR_Produkten.tex
The translation was initiated by on 1999-11-18
Fußnoten
- ... Residualvarianz
![[*]](foot_motif.gif)
- Hierbei ist anzumerken, dass es für die spätere Bewertung nicht notwendig ist,
die Residualvarianz
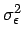 und im weiteren Verlauf den
Parameter
und im weiteren Verlauf den
Parameter 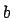 zu berechnen.
zu berechnen.
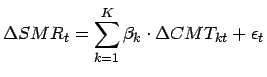
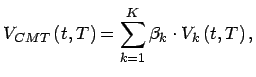
![$\displaystyle P\left( t,T\right) \cdot \left[ f-\frac{1}{2}\cdot f^{2}\cdot \si...
...-h\right) \cdot \frac{PV''_{N}\left( f\right) }{PV'_{N}\left( f\right) }\right]$](img39.gif)